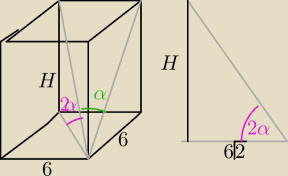
stereometria MalWas: Pole podstawy graniastosłupa prawidłowego czworokątnego jest równe 36. Kąt nachylenia przekątnej graniastosłupa do płaszczyzny ściany bocznej ma miarę α. Kąt nachylenia tej przekątnej do płaszczyzny podstawy jest równy 2α. Oblicz pole powierzchni graniastosłupa.

a7: P_c=2*36+4*6*H tg2α=H/(6√2) czyli H=tg2α*6√2 P_c=72+144√2tg(2α)

MalWas: <3 Dziękuję

Tadeusz: ... to trochę nie tak układ dwóch równań i wyznaczysz miarę kąta α

a7: właśnie się doliczyłam

a7: nie, nie doliczyłam się

Bogdan:

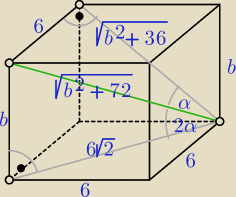
	6		√ b2 + 36
sinα =		, cosα =
	√ b2 + 72		√ b2 + 72

	12√b2 + 36
sin2α = 2sinα cosα =
	b2 + 72

b		b		12√b2 + 36
	= sin2α ⇒		=
√ b2+72		√ b2+72		b2 + 72

Po rozwiązaniu ostatniego równania otrzymamy wartość b

mr t: i b wychodzi niewymierne...

a7: a to nie szkodzi

a7: a ile wyszło?

mr t: liczyłem tę rąbankę w mathway'u i podali tylko przyblizenie rowne 10.79

mr t: Natomiast sam próbowałem to ogarnąc z tw sin i cos i rowniez dochodziłem do jakis dziwadeł

a7: b=6√(1+√5) czyli Pc=72+4*6*6√(1+√5)=...72(1+2√(1+√5))

a7: b(b²+72)=12√(b²+36)(b²+72) b²(b²+72)²=144(b²+36)(b²+72) b⁴+72b²=144b²+5184 b⁴−b²−51840= b²=t i t>0 Δ=25920=5*72*72 √Δ=72√5 b²=36(1+√5 b=6√(1+√5)

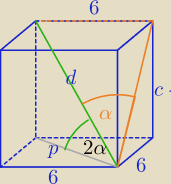
Mila: Mam takie rachunki. p=6√2 1)

	6		36
sinα=		⇔sin2α=
	d		d2

	6√2		6√2
cos2α=		⇔1−2sin2α=
	d		d

	72		6√2
1−		=		⇔d2−6√2d−72=0
	d2		d

d=3(√2+√10) c=6√1+√5 z tw. Pitagorasa

Mila: No to mamy zgodność wyników

a7: