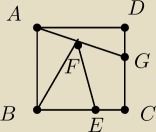
 Kwadrat podzielno na cztery częsci o równych polach tak jak na rysunku. Oblicz stosunek BE:EC.
Kwadrat podzielno na cztery częsci o równych polach tak jak na rysunku. Oblicz stosunek BE:EC.
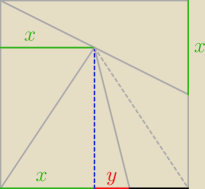

 z podobieństwa trójkątów
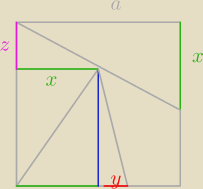
U{a}{a]{2}}=U{u{a2]{z}
z podobieństwa trójkątów
U{a}{a]{2}}=U{u{a2]{z}
| 1 | ||
czyli z= | a | |
| 4 |
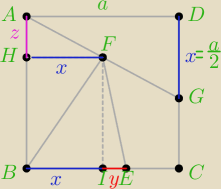 bok kwadratu to a , |DG|=x
pole trójkąta ADG=1/2ax czyli jedna czwarta pola kwadratu a2
1/2*a*x=1/4*a2 stąd wychodzi, że x jest równe połowie a x=1/2*a
zauważamy że skoro pola wszytskich figur są równe to |HF| też równe x gdyż pola trójkątów muszą
być równe a mają tą samą podstawę równą a)
|BI| też równe x
następnie z podobieństwa trójkątó ADG i AHF wychodzi, że z=1/4*a
następnie pole trójkąta AHF musi być równe polu trójkąta FEI
czyli y=1/6*a
czyli szukany stosunek BE:EC wynosi
bok kwadratu to a , |DG|=x
pole trójkąta ADG=1/2ax czyli jedna czwarta pola kwadratu a2
1/2*a*x=1/4*a2 stąd wychodzi, że x jest równe połowie a x=1/2*a
zauważamy że skoro pola wszytskich figur są równe to |HF| też równe x gdyż pola trójkątów muszą
być równe a mają tą samą podstawę równą a)
|BI| też równe x
następnie z podobieństwa trójkątó ADG i AHF wychodzi, że z=1/4*a
następnie pole trójkąta AHF musi być równe polu trójkąta FEI
czyli y=1/6*a
czyli szukany stosunek BE:EC wynosi
| x+y | |
=(4/6*a):(2/6*a)= 2:1 | |
| a |
| x+y | ||
jeszcze poprawka |BE| : |EC|= | =2:1 | |
| a−x−y |