monotonicznosc mr t :

	4x
Wyznacz przedziały monotoniczności funkcji f(x)=
	x2+1

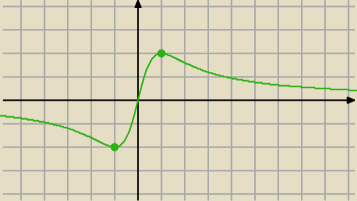
a7: trzeba policzyć pierwszą pochodną i przyrównać do zera (licznik, gdyż mianownik pochodnej będzie równy (x²+1)² i jest zawsze dodatni to jest pochodna będzie zmieniała znak tak jak licznik)

mr t : Tak tez zrobiłem, tylko interesuje mnie czemu funkcja przyjmuje wartości dodatnie dla x∊(−1;1) a nie dla <−1;1> ?

mr t : Ma to jakiś związek z tym, ze w tych punktach wystepuja lokalnie wartośc najmniejsza i największa?

f123: Funkcja nie przyjmuje wartosci dodatnich dla x ∊ (−1, 1), tylko w tym przedziale jest rosnaca

PW: Do pytania z 17:11 Twierdzenie o monoroniczności funkcji różniczkowalnej jest sformułowane dla przedziału otwartego.

f123: @PW jesli w poleceniu mamy wyznaczyc maksymalne przedzialu monotonicznosci funkcji, powinnismy uzywac nawiasow domknietych?

wredulus_pospolitus: nie ... nie używamy domkniętych ... jedyne co to 'włączamy' do przedziału punkty przegięcia (x = 0 w tym przypadku)

f123: Byla na discordzie o tym kiedys dyskusja

PW: Jest to bardziej subtelne rozumowanie niżby się wydawało. Funkcja jest malejąca na przedziale (1,+∞), bo ma na tym przedziale pochodną ujemną. Funkcja jest także ciągła (to wiemy skądinąd), a więc lim f(x) = f(1) x→1+ i f(1) jest największą wartością funkcji na tym przedziale, więc można odpowiedzieć, że f jest malejąca na <1,+∞). Wystarczyłoby powiedzieć, że jest rosnąca na (0,1) i malejąca na (1,+∞) − jako funkcja ciągła nie ma innego wyjścia − liczba f(1) jest maksimum lokalnym, a więc można sobie podomykać przedziały monotoniczności w 1.

mr t: PW, czy dobrze w takim razie rozumiem, że funkcja maleje na przedziale (−∞;−1> i <1;∞) ?

PW: No tak, ale zazwyczaj opowiada się o monotoniczności na przedziałach otwartych (moim zdaniem nie będzie błędu, jeśli powiemy, że jest malejąca na przedziale (−∞, −1) i malejąca na przedziale (1,+∞). Toczenie sporów o ten jeden punkt na krańcu nie jest potrzebne − po narysowaniu wykresu (gdzie rośnie, gdzie maleje) widać, czy ten punkt można dołączyć do przedziału, na którym rośnie (maleje), a w przypadku funkcji ciągłej można go dołączyć zarówno do przedziału, na którym rośnie, jak i do przedziału, na którym maleje.

mr t : Okej, dzięki