Liczba rozwiązań Różniczka: Proszę o wyjaśnienie liczby rozwiązań: lnx=x+a x>0 f(x) = lnx−x−a f(x)'=1/x−1 f(x)'>0 x∊(0,1) f(x)'=0 x=1 f(x)'<0 x>1 max x=1 f(1)=−1−a Nie rozumiem tego fragmentu: 1 rozw. a=1 0 rozw. a>−1 2 rozw. a<−1

wredulus_pospolitus: powiem tak −−−− tragiczny sposób podejścia do zadania

Różniczka: Właśnie przepisuję notatki od kolegi i zastanawiam się nad sensem.

wredulus_pospolitus: g(x) = lnx <−−−− wyznacz wzór ogólny STYCZNEJ do g(x) następnie wyznacz taką styczną do g(x), aby jej współczynnik kierunkowy był równy '1' porównaj wzór tejże stycznej do h(x) = x + a wyciągnij wnioski

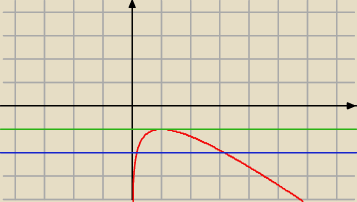
ABC: zobacz sobie to na wykresie ln(x)−x=a

Różniczka: Czy styczna to nie po prostu pochodna?

wredulus_pospolitus: albo ... f(x) = lnx − x

	1
f'(x) =		− 1
	x

f_max = −1 (dla x = 1) więc równanie: f(x) = a czyli lnx − x = a czyli lnx = x + a ma jedno rozwiązanie dla a = −1 ma zero rozwiązań dla a > −1 (bo f_max = −1 ) ma dwa rozwiązania dla a < −1 <−−− to już z monotoniczności mamy

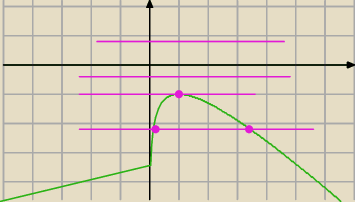
a7: powyżej na zielono narysowany wykres funkcji y=lnx−x (wykres idzie w lewo w bok od pewnego miejsca , to jakiś bug/błąd w programie?) a na różowo y=a ilość rozwiązań (punktów przecięcia obu wykresów) jest zero jeśli a jest większe niż minus 1 (a>−1) jedno rozwiązanie , gdy a=−1 dwa rozwiązania, gdy a<−1

ABC: no właśnie mówię że to klasyczny sposób: zbadać funkcję ln(x)−x i ciąć prostymi równoległymi do osi OX

Różniczka: Dzięki, już rozumiem. Teraz mam kłopot z fragmentem: ln(x)=−x+a f(x)=lnx+x−a f(x)'=1/x+1>0 lim_x→0f(x)=−∞ jedno rozwiązanie Prosiłbym o wytłumaczenie

Różniczka: Ach, x>0 w powyższym.