rozwiąż nierówność Beata: rozwiąż nierówność:

x		x
	+		≥2
x+1		x−2

Mickej: najlepiej sprowadzić do wspólnego mianownika

x(x−2)+x(x+1)−2(x−2)(x+1)
	≥0
(x−2)(x+1)

teraz wymnażasz licznik wyznaczasz jego miejsca zerowe zapisujesz licznik w postaci iloczynowej miejsc zerowych funkcji a na koniec przechodzisz na postać ułamka zaznaczasz miejsca zerowe na osi liczbowej i wyznaczasz przedziały dla których f(x)≥0

Godzio:

x(x−2) + x(x+1)
	≥ 2
(x+1)(x−2)

x2 − 2x + x2 +x
	≥ 2
(x+1)(x−2)

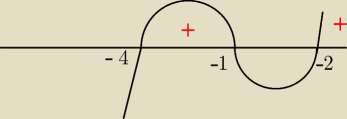
(2x² −x)(x+1)(x−2) ≥2(x+1)²(x−2)² (2x² −x)(x+1)(x−2) − 2(x+1)²(x−2)² ≥ 0 (x+1)(x−2)(2x²−x − 2(x+1)(x−2) ) ≥ 0 (x+1)(x−2)(2x²−x − 2(x²−x−2) ≥ 0 (x+1)(x−2)(2x²−x − 2x² + 2x+4) ≥ 0 (x+1)(x−2)(x+4) ≥ 0 x = −1 x = 2 x = −4 x∊<−4,−1> ∪ x∊<−2,∞)