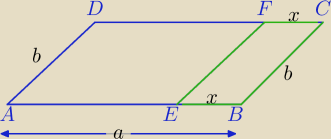
Dany jest rownoleglobok Agatka: Dany jest równoległobok ABCD o bokach lABl = a i lBCl = b. Czworokąt EBCF jest równoległobokiem podobnym do równoległoboku ABCD. Wykaż że obwód czworokąta AEFD jest równy (2a² − 2b²)/a + 2b Nie mam pojęcia jak to zrobić. Pomoże ktoś zrozumieć?

Mila: 1) Z podobieństwa równoległoboków:

x		b		b2
	=		⇔x=
b		a		a

	b2
L=2b+2*(a−		)=...
	a

oliwia:

Mila:

	(a2−b2)
L=2b+2*
	a