wektory bob: O jaki wektor należy przesunąć funkcję f(x)=x³+1, aby otrzymać funkcję g(x)=x³−6x²+12x+8. Ktoś ma jakiś pomysł?

wredulus_pospolitus: x³ − 6x² + 12x + 8 = x³ − 3x²*2 + 3*x*2² − 8 + 16 = (x−2)³ + 16 Dalsze wnioskowanie pozostawiam Tobie

bob: okej, będzie to wektor [2,15]. Strasznie topornie idzie mi ten typ zadań. Wiem, że to jest dosyć banalny przykład, ale miałem problem, żeby algebraicznie ustalić o jaki wektor trzeba przesunąć funkcję f(x)=2x+3, żeby otrzymać g(x)=2x−3 (xD). Mógłbyś wytłumaczyć?

Jerzy: Przesuwasz wykres o 6 jednostek w dół wdłuż osi OY , czyli o wekror [0,−6]

bob: no właśnie w odpowiedziach jest [2:−2] i jak się to podstawi pod wzór pierwszej funkcji to wychodzi dobrze, więc to chyba nie tak jednak.

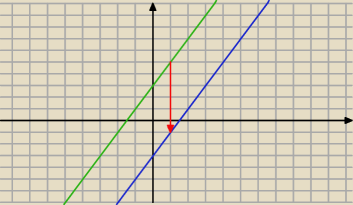
Jerzy: Jakie Twoim zdaniem współrzędne ma czerwony wektor ?

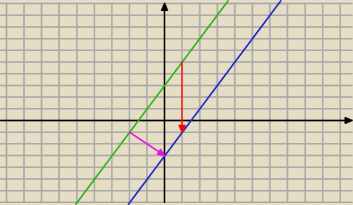
Jerzy: Jest ok , bo wektor fioletowy ma właśnie współrzędne [2,−2]

bob: Tzn chyba obie wersje są poprawne. W podręczniku po prostu podali drugą wartość −2 i trzeba było dojśc to tej pierwszej i w tedy to faktycznie jest 2.

Jerzy: Jeśli v = [2,2] , to mamy: g(x) = 2(x − 2) + 3 − 2 = 2x − 4 + 1 = 2x − 3 Jeśli v = [0,−6] , to mamy: g(x) = 2(x − 0) + 3 − 6 = 2x − 3 czyli dokładnie to samo.

Jerzy: W pierwszej linice oczywiście v = [2,−2]