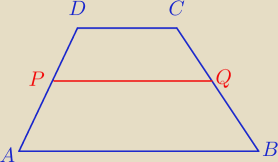
w trapezie abcd o podstawach ab i cd poprowadzono odcinek Marta: w trapezie abcd o podstawach ab i cd poprowadzono odcinek pq o dlugosci √ab rownolegy do podstaw trapezu. Uzasadnij że A) lAPl/lPDl = AB/PQ B) trapezy ABQP i PCQD są podobne Nie mam kompletnie pojęcia jak się zabrać do tego

Marta: Up

janek191: Czy I PQ i = √ I AB I ? czy raczej I AB I = a i I CD I = b i I PQ I = √a*b ?

Marta: Ta druga opcja l AB l = a

Marta: Pomoże ktoś?:(

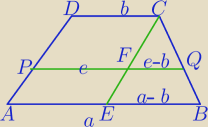Mila: a) Z. PQ||AB, |PQ|=√a*b

	lAPl		AB
T.		=
	lPDl		PQ

=================== CM||AD, |PQ|=e 1) e=√a*b⇔e²=a*b⇔

a		|AB|		e		√ab
	=		=		=
e		|PQ|		b		b

2)ΔFQC∼ΔEBC⇔

|FC|		|CE|
	=		, |FC|=|PD|, |CE|=|AP|+|PD|
e−b		a−b

PD		|AP|+|PD|
	=		⇔
e−b		a−b

|PD|		e−b		|AP|+|PD|		a−b
	=		⇔		=
|AP|+|PD|		a−b		|PD|		e−b

|AP|		a−b		|AP|		a−b
	+1=		⇔		=		−1 po przekształceniu
|PD|		√ab−b		|PD|		√ab−b

|AP|		√ab
	=		⇔
|PD|		b

|AP|		|AB|
	=
|PD|		|PQ|

cnw b) Skorzystaj z równości odpowiednich kątów i proporcji z (a)

Mila: Oj, coś Marta reaguje z opóźnieniem

Agatka: Jakoś nie zrozumiałe jest to kompletnie dla mnie

Marta: Skąd się wzięło to −1 i +1?

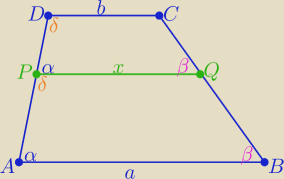Eta: Mamy równość miar kątów w tych trapezach

	a		x
i x=√ab 2 ⇒ x2=ab ⇒		=
	x		a

zatem trapezy są podobne ( odp. do b)

	|AP|		|AB|
to:		=
	|PD|		|PQ|

to wszystko !