Podaj rozwiązanie nierówności należące do przedziału <0,2π> tako: Tak jak w opisie zadania: podaj rozwiązanie nierówności z przedziału <0,2π>

	x
a) tg		< 1
	2

b) |tg x| ≥ √3 Z góry dziękuję za rozwiązanie

Godzio:

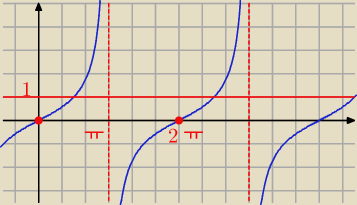
	x		x		π
tg(		) = 1 ⇔		=		+ kπ gdzie k ∊ C
	2		2		4

	π
x =		+ 2kπ
	2

	π
x1 =		(dla k = 0)
	2

	5
x2 =		π (dla k = 1)
	2

Z wykresu odczytujemy rozwiązanie:

	π
x ∊ <0,		) U (π,2π>
	2

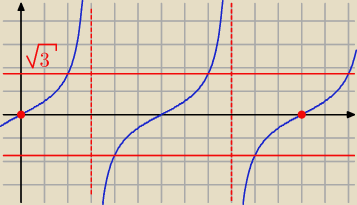
Godzio: |tg(x)| ≥ √3 ⇔ tg(x) ≥ √3 lub tg(x) ≤ − √3

	π
tg(x) = √3 ⇔ x =		+ kπ
	3

	π
tg(x) = −√3 ⇔ x = −		+ kπ gdzie k ∊ C
	3

Kolejne rozwiązania (idąc od lewej)

	π
x1 =		(k = 0, pierwsze równanie)
	3

	2
x2 =		π (k = 1, drugie równanie)
	3

	4
x3 =		π (k = 1, pierwsze równanie)
	3

	5
x4 =		π (k = 2, drugie równanie)
	3

Odczytujemy:

	π		2		4		5
x∊ <0,		> U <		π,		π> U <		π,2π>
	3		3		3		3

tako: Mam pytania do a). x ∊ <0,pi/2) U{skąd to?} (pi, 2pi> dlaczego tg x/2 = 1, a nie tg x/2 > 1?

tako: Dobra rozumiem skąd to co wyżej napisałem, ale dlaczego u ciebie granica przebiega w x=pi a nie x=pi/2

tako: Aaa, bo wykres narysowany to tg x/2, czyli poszerzył się, dobra dzięki.