trapez Kasia: W trapezie ABCD o podstawach AB=a i DC=b poprowadzono dwa odcinki MN i KL równoległe do podstaw,które podzieliły trapez na trzy figury o równych polach. Wyznacz długości tych odcinków.

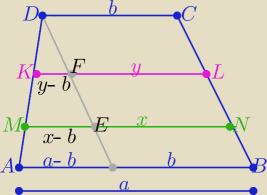
Eta: Z podobieństwa trójkątów i równości pól mamy:

	a−b		3(y+b)		a2+2b2
		=		⇒..... y=√
	y−b		a+b		3

	a−b		3(x+b)		2a2+b2
i		=		⇒ .....x=√
	x−b		2(a+b)		3

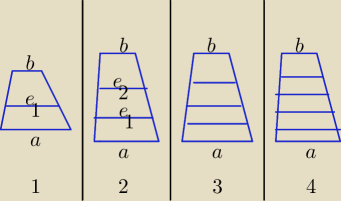Bogdan: e₁, e₂, e₃, e₄, ... , e_n − długości odcinków dzielących trapez na trapezy o równych polach patrząc od strony podstawy długości a, czyli pierwszy odcinek nad a to e₁. Można skorzystać tu z faktu: odcinek równoległy do podstaw trapezu i dzielący go na dwa trapezy o równych polach ma długość równą średniej kwadratowej długości podstaw a, b. 1. 2 trapezy: e₁ = √ (a² + b²) / 2 2. 3 trapezy: e₁ = √ (a² + e₂²) / 2, i e₂ = √ (e₁² + b²) / 2 stąd 2e₁² = a² + e₂² i 2e₂² = e₁² + b² po rozwiązaniu tego układu równań mamy: e₁ = √ (2a² + b² / 3} i e₂ = √ (a² + 2b²) / 3. Postępując analogicznie otrzymamy: 3. 4 trapezy: e₁ = √ (3a⁴ + b²) / 4, e₂ = √ (2a² + 2b²) / 4, e₃ = √ (a² + 3b²) / 4 4. 5 trapezów: e₁ = √ (4a⁴ + b²) / 5, e₂ = √ (3a² + 2b²) / 4, e₃ = √ (2a² + 3b²) / 4, e₄ = √ (a² + 4b²) / 5 Widać regularność, można więc zapisać wzory na długości kolejnych odcinków dzielących trapez na n części o równych polach: k−ty odcinek patrząc od dołu (od a): e_k = √ ((n − k)a² + kb²) / n

Godzio: Dobry wieczór Bogdanie! Jak zwykle warte uwagi rozwiązanie