stereometria
f123: Ostroslup ABCD o podstawie trojkatnej ABC ma krawedzie boczne o dlugosciach |AD| = a, |BD| = b,
|CD| = c i katy proste miedzy tymi krawedziami Oblicz objetosc tego ostroslupa. Uzasadnij ze
wysokosc tego ostroslupa opuszcona na podstawe ABC ma dlugosc
28 kwi 16:07
f123: | | 1 | |
czy V to po prostu |
| abc  |
| | 6 | |
28 kwi 16:15
Mila:
Tak.
| | 1 | | 1 | | 1 | |
VABCD= |
| * |
| ab*c= |
| abc |
| | 3 | | 2 | | 6 | |
28 kwi 17:24
Mila:
Policzyłeś dalej ?
28 kwi 18:52
f123: Dzieki za sprawdzenie, nie, dopiero okolo 21 bede znowu probowal. Do wykazanie tego, lepiej
przyjac ze podstawa ostroslupa jest trojkat o bokach a, b, c?
28 kwi 19:47
Mila:
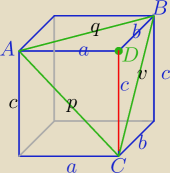
Masz wykazać , że dł. wysokości opuszczonej na ΔABC wyraża się podanym wzorem.
Popatrz na rysunek.
Objętość tego naroża oblicza się bardzo prosto, z pole ΔABC jest kłopot.
aby z tego wzoru wyznaczyć H musisz obliczyć P
ΔABC o bokach p,q,v.
Powodzenia.
28 kwi 21:28
Saizou :
Rysunek
Mili, zatem
p
2=a
2+c
2
q
2=a
2+b
2
v
2=b
2+c
2
NIech α = ∠ACB, wówczas z tw. cosinusów
q
2=p
2+v
2−2pccosα
....
Z jedynki trygonometrycznej
| | √a2b2+a2c2+b2c2 | |
sinα= |
| |
| | √a2+c2(b2+c2) | |
| | 1 | | √a2b2+a2c2+b2c2 | |
P = |
| √a2+c2√b2+c2* |
| |
| | 2 | | √a2+c2(b2+c2) | |
P =
√a2b2+a2c2+b2c2
28 kwi 21:41
Mila:
Trochę inaczej obliczyłam, ale też wyszło
28 kwi 22:05
Saizou :
Tak z ciekawości, jak liczyłaś Milu?
28 kwi 22:10
Mila:
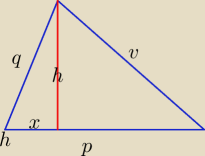
1)
p
2=a
2+c
2 , q
2=a
2+b
2, v
2=b
2+c
2
2)
h
2=q
2−x
2
h
2=v
2−(p−x)
2
q
2−x
2=v
2−p
2+2px−x
2
| | q2+p2−v2 | |
x= |
| po podstawieniu |
| | 2p | |
| | a4 | | a2c2+a2b2+b2c2 | |
h2=a2+b2− |
| = |
| |
| | a2+c2 | | a2+c2 | |
3)
| | 1 | | √a2c2+a2b2+b2c2 | |
PΔ= |
| *√a2+c2* |
| |
| | 2 | | √a2+c2 | |
=========================
28 kwi 22:26
Saizou :
będzie dla potomnych
28 kwi 22:36