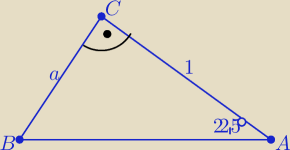
Jeden z kątów ostrych trójkąta prostokątnego ma miarę 22,5°. oblicz Marta: Jeden z kątów ostrych trójkąta prostokątnego ma miarę 22,5°. oblicz długość krótszej przyprostokątnej tego trójkąta jeśli dłuższa przyprostokątna ma długość równą 1. Rozrysowalem sobie ten trójkąt i pozaznaczalem katy. Trzeba to zadanie zrobić z twierdzenia o dwusiecznej kąta. Ale w jaki sposób mam to zrobić jeśli jest tylko 1 bok podany? Wiem że w środku trójkąta dwusieczna stworzy jeden trójkąt równoramienny ale co dalej?

a7: a gdzie jest ten trójkąt równoramienny? i dlaczego akurat z tw. o dwusiecznej?

Marta: Dwusieczna dzieli kat na pół czyli wychodzi trójkąt o bokach 67.5 45 67.5 Z twierdzenia tego ponieważ zadanie jest z tego tematu a sin i cos nie ma jeszcze na tym poziomie

Marta: Up

a7: ok mam

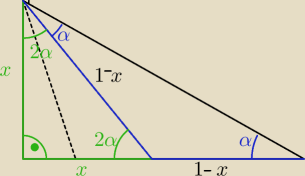
a7: z tw. Pitagorasa 1−x=x²+x² 2x²+x−1=0 Δ=9 √Δ=3

	1
x=		(x2 jest mniejsze od zera więc sprzeczne)
	2

========

Marta: Odpowiedź w książce to √2 − 1. Delty też nie ma jeszcze na tym poziomie książki Rysunek mi też się jakoś nie zgadza. Mowa jest o dwusiecznej która dzieli kat na pół a nie na 2a i 1a

a7: widzę błąd (1−x)²=2x² 1−2x+x²=2x² x²+2x−1=0 Δ=12 √Δ=2√3 x=√3−1

Marta: Nadal odpowiedzi się nie zgadzaja

a7: rozumiem, ja inaczej nie umiem tego policzyć, może jeszcze zabierze głos ktoś inny i poda inne rozwiązanie

Marta: Już rozumiem delta = 8 a nie 12

Marta: Dęta = 4 + 4 = 8 Wtedy X2= −2+2√2/2 X2= −1+√2 co daje √2 −1

a7: ok mam wyszło

a7: moment

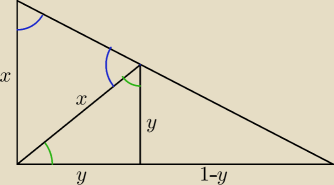
a7: z podobieństwa trójkątów

1−y		1
	=
y		x

z twierdzenia Pitagorasa x²=2y² ⇒x=y*√2 wymnażamy pierwsze na krzyż

	√2
(1−y)yp{2]=y ⇒ y2√2+y√2=y=0 czyli y(y√2+√2−1)=0 y=1−
	2

	√2
x=y√2 czyli x=(1−		)*√2=√2−1
	2

================================

a7: może będzie ktoś kto wychwyci gdzie jest błąd w pierwszym sposobie albo jeszcze poda inny sposób

a7: aj przepraszam, rzeczywiście żle policzona delta i się zgadza obydwoma sposobami

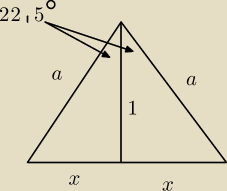
ICSP: x² + 1 = a² 2x = a²sin(45^o) x² + 1 = 2√2x x² − 2√2x + 2 = 1 (x − √2)² = 1 x = √2 − 1 v x = √2 + 1 czyli x = √2 − 1

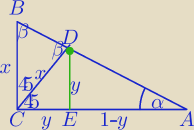
Mila: Bez równania kwadratowego. α=22.5 β=67.5 1) ΔCED− Δprostokątny równoramienny ΔBDC−Δ równoramienny, |CD|=x

	x
x=√2y ⇔y=
	√2

2) ΔDEA∼ΔBCA⇔

y		x
	=		⇔y=x−xy ⇔y+xy=x
1−y		1

y*(1+x)=x

	x
y=
	x+1

x		x
	=
√2		x+1

1		1
	=
√2		x+1

x+1=√2 x=√2−1 ======

Eta:

	2tgα
a= tg22,5o ze wzoru : tg 2α=
	1−tg2α

	2a
to tg45o=1 =		⇒ a2+2a+1=2 ⇒ (a+1)2=2 i a>0 ⇒a+1=√2
	1−a2

a= √2−1 ========

Mila: Nie miała funkcji trygonometrycznych.

Eta: @Mila Skąd to wiesz?

Eta: Marta , to chłopak −maturzysta

ABC: życie to nie bajka, Marta ma dwa jajka

Eta: