Konstrukcje geometryczne Ola: Dane są trzy odcinki długości 1,a i b. Skonstruować za pomocą cyrkla i linijki odcinki długości ab,a/b i √a. Niestety nie mam pojęcia, jak zabrać się za to zadanie. Kroki konstrukcji to : 1.Analiza zadania 2.Opis konstrukcji 3.Dowód poprawności konstrukcji 4.Badanie warunków istnienia i liczby rozwiązań Z góry bardzo dziękuję za pomoc.

a7: http://www.math.uni.wroc.pl/~swiatkow/konstr/skrypt_konstr.pdf

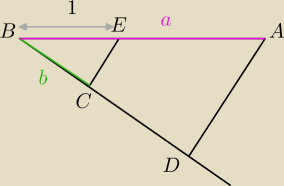
a7: na podstawie linku AD||EC z tw. Talesa

|BE|		|BA|
	=
|BC|		|BD|

1		a
	=		⇒ |BD|=a*b
b		|BD|

Ola: Udało mi się zrobić tyle. Nie wiem natomiast jak zrobić pozostałe punkty: 1.Analiza zadania i 4.Badanie warunków istnienia i liczby rozwiązań. Z góry bardzo dziękuję. https://scontent.fwaw5-1.fna.fbcdn.net/v/t1.15752-9/95264577_1359315880918448_7922070695050215424_n.png?_nc_cat=103&_nc_sid=b96e70&_nc_ohc=Uw6I93bmSqcAX-RQX4J&_nc_ht=scontent.fwaw5-1.fna&oh=dcd6838c2a0660d5d71308e38cf24e28&oe=5ED08EF9 Opis konstrukcji odcinka ab 1.Kreślimy dwie proste l i m przecinające się w punkcie S 2.Na prostej m umieszczamy odcinek jednostkowy SD oraz odcinek b=DC o początku w punkcie D i w kierunku przeciwnym do S 3.Na prostej l umieszczamy odcinek a=SA 4.Rysujemy odcinek AD 5.Konstrukcyjnie rysujemy odcinek równoległy do odcinka AD przechodzący przez punkt C: −Niech prosta k będzie przedłużeniem odcinka AD −Rysujemy łuk o środku C, przecinający prostą k w dwóch punktach E i F −Rysujemy łuk o środku C i promieniu EF, łuk o środku C i promieniu CE=CA oraz punkt ich przecięcia – G −Rysujemy prostą n przechodzącą przez punkty C i G oraz umieszczamy punkt B będący punktem przecięcia prostych n i l Odcinek CB jest odcinkiem równoległym do odcinka AD, a odcinek AB oznaczmy jako x Dowód poprawności konstrukcji odcinka ab Korzystając z twierdzenia Talesa możemy ułożyć równanie: SA/SD=ABC a:1=x:b x=ab https://scontent.fwaw5-1.fna.fbcdn.net/v/t1.15752-9/95349126_245068333384133_8657714067898630144_n.png?_nc_cat=100&_nc_sid=b96e70&_nc_ohc=nCOTdZSkQloAX-YRBOb&_nc_ht=scontent.fwaw5-1.fna&oh=2a2ce0031ae0748994fd9b7ae86110a3&oe=5ED0D2B1 Opis konstrukcji odcinka a/b 1.Kreślimy dwie proste l i m przecinające się w punkcie S 2.Na prostej m umieszczamy odcinek jednostkowy SD 3.Na prostej l umieszczamy odcinek b=SA odcinek a=AB o początku w punkcie A i w kierunku przeciwnym do punktu S 4.Rysujemy odcinek AD 5.Konstrukcyjnie rysujemy odcinek równoległy do odcinka AD przechodzący przez punkt B: −Niech prosta k będzie przedłużeniem odcinka AD −Rysujemy łuk o środku C, przecinający prostą k w dwóch punktach E i F −Rysujemy łuk o środku w punkcie B i promieniu EF, łuk o środku F i promieniu EB=BF oraz punkt ich przecięcia – G −Rysujemy prostą n przechodzącą przez punkty C i G oraz umieszczamy punkt C będący punktem przecięcia prostych n i m Odcinek CB jest odcinkiem równoległym do odcinka AD, a odcinek DC oznaczmy jako y Dowód poprawności konstrukcji odcinka a/b Korzystając z twierdzenia Talesa możemy ułożyć równanie: SA/SD=AB/DC b:1=a:y y=a/b https://scontent.fwaw5-1.fna.fbcdn.net/v/t1.15752-9/95136915_265786237937333_5328238059781619712_n.png?_nc_cat=101&_nc_sid=b96e70&_nc_ohc=kcIGfQWm8doAX_ziILX&_nc_ht=scontent.fwaw5-1.fna&oh=6352e883fb0c1a6a32e6b0565a479af3&oe=5ED1AA55 Opis konstrukcji odcinka √a 1.Kreślimy prostą m, na której umieszczamy odcinki a=OA oraz odcinek jednostkowy AB zaczynając od A i w kierunku przeciwnym do O 2.Wyznaczamy konstrukcyjnie środek odcinka OB, rysując łuki o środkach w punktach A i B i jednakowym promieniu takim, aby przecięły się w punktach E i F (czyli o promieniu dłuższym od długości połowy odcinka AB) 3.Kreślimy prostą k przechodzącą przez punkty E i F i punkt przecięcia S prostej m i prostej k 4.Kreślimy okrąg, o środku w punkcie S, którego średnicą jest odcinek OB. 5.Przez punkt A prowadzimy prostą prostopadłą do OB, która przetnie okrąg w punkcie C. −rysujemy łuk o środku w punkcie A i promieniu takim, by przeciął prostą m w dwóch różnych punktach ( na naszym rysunku w punktach B i D) −rysujemy łuki o tym samym promieniu i środku odpowiednio w punktach B i D takim, aby przecięły się w punktach G i H (czyli o promieniu dłuższym od długości połowy odcinka BD) −rysujemy prostą GH, która jest prostopadła do odcinka OB, przechodzi przez punkt A oraz przecina okrąg w punkcie C 6.Rysujemy trójkąt OBC, w którym kąt OCB jest prosty zgodnie z twierdzeniem geometrii elementarnej, głoszącym, że kąt wpisany w okrąg oparty na średnicy jest kątem prostym. Dowód poprawności konstrukcji odcinka √a Należy zauważyć, że trójkąty OBC, OAC i CAB są podobne zgodnie z cechą podobieństwa trójkątów kąt−kąt−kąt, gdyż ∢ OCB= ∢ CAO= ∢ CAB=90, ∢ CBO = ∢ OCA= ∢ CBA a co za tym idzie ∢ COB= ∢ COA= ∢ OCB Niech AC=x, a więc z podobieństwa trójkątów mamy: 1/x=x/a x2=a x=√a