Planimetria bartek: Stosunek dwóch boków równoległoboku jest równy 3:4, a jego przekątne mają długości 15 i 35. Oblicz długości boków równoległoboku

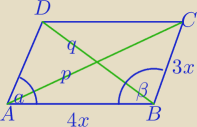
Mila: Twierdzenie cosinusów.

bartek: jeszcze jakaś podpowiedź?

a7: cosβ=cos(180−α)=−cosα

wredulus_pospolitus: 35² = 25x² + 24x²*cosα 15² = 25x² − 24x²*cosα wyznaczasz 'x' i przy okazji cosα

a7:

⎧	225=9x2+16x2−12x2cosα
⎩	1225=9x2+16x2+12x2cosα

a7: oj pomyłka ("cyfrówka" )zamiast 12 powinno być 24

a7: z pierwszego mamy że 24x²cosα=25x²−225 wstawiamy do drugiego i mamy 1225=25x²+25x²−225 x²=25 x=5 3x=15 4x=20 ============

bartek: Dziękuję

a7:

Eta: W każdym równoległoboku : f²+e²= 2a²+2b² a=4x, b=3x , x>0 i f=35, e=15 to: 1225+225= 50x² ⇒ x²=29 ⇒ x= √29 Odp: a=4√29 , b= 3√29 =====================

Eta: @a7 1225=25x²+25x²−225 ⇒ x²=29

a7: tak, no właśnie byk na byku

Eta: