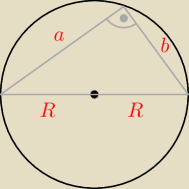
Okrąg, trójkąt prostokątny Szkolniak: W okrąg o(O,R) wpisać trójkąt prostokątny taki, aby promień r okręgu wpisanego w ten trójkąt był możliwie największy.

	ab		r(a+b+c)		a+b−c
P=		i P=		, r=
	2		2		2

Próbowałem coś z równości pól, Pitagorasa, ale coś mi to nie idzie.. Mógłbym prosić o wskazówkę, czy dobrze kombinuję?

wredulus_pospolitus:

	b
sinα =		−−−> b = 2R*sinα
	2R

	a
cosα =		−−−> a = 2R*cosα
	2R

c = 2R

	2P		4R2sinαcosα
więc r =		=
	a+b+c		2R(sinα + cosα + 1)

szukasz maksimum w zależności od 'α' (α = π/4 powinna Ci wyjść)

Saizou : a²+b²=4R²

	a+b−c		a+b−2R		a+b
r=		=		=		−R
	2		2		2

	a+b
r−R=
	2

Kw ≥ Am

	a2+b2		a+b
√		≥
	2		2

	4R2
√		≥ r−R
	2

R√2 ≥ r−R R(√2−1) ≥ r r=R(√2−1)

Mila: 2) a+b=2R+2r

	π
r(α)=R(sinα+cosα−1) i α∊(0,		)
	2

Szkolniak:

	π
Wyszło		, wredulus
	4

Saizou Dlaczego między druga a trzecią linijka, przy przenoszeniu 'R', nie zmieniłeś przy nim znaku?

Saizou : "znakówka"

Szkolniak: To ciekawe, bo w odpowiedziach u siebie w książce również mam taką odpowiedź jak ty podałeś

Saizou : Haha, ciekawe

Saizou : bo wcześniej mam błąd

	a+b
r+R=
	2

zatem odp. z książki jak i u mnie jest dobra (chociaż u mnie przypadkowo)

Szkolniak: No i teraz pasuje, dzięki za pomoc