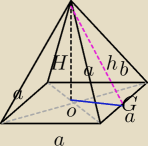
zadanie optymalizacyjne jaros: Oblicz największe możliwe pole powierzchni bocznej ostrosłupa prawidłowego czworokątnego o

	4√2
objętości równej		.
	3

Zadanie chciałbym rozwiązać sam a tutaj przychodzę w sprawie konsultacji czy moja idea jest dobra. Więc;

	a
1) Zauważamy, że |OG| =
	2

	1
2) Wyznaczam pole do oraz jego wzór, który będę chciał optymalizować: Pb =		* hb * a
	2

	4√2		1
3) Ze wzoru na objętość wyznaczam równanie		=		*a2*H
	3		3

	4√2
4) H =
	a2

	a
4) wyznaczam hb z tw. Pitagorasa: więc hb = √H +
	2

	1		4√2		a
Otrzymuje funkcje pola bocznego =		* √		+		* a
	2		a2		2

Pod ostanim funkcja ma pierwiastek i teraz mam takie pytanie, czy to co napisałem ma sens?

salamandra:

	a
w 4) powinno być hb=√H+
	4

salamandra:

	a
a raczej nawet H2+
	4

jaros: a tak racja, ale optymalizował byś tą funkcje już?

jaros: O ile coś takiego na naszym poziomie jest możliwe bo nie wiem czy nie powstaje funkcja złożona

f123: Co za problem wziac wyrazenie pod pierwiastkiem i przyjac to jako funkcja zmiennej 'a' i wtedy optymalizowac?

salamandra: zaraz rozwiążę

jaros: Ktoś pomoże znaleźć mi błąd w funkcji optymalizowanej? bo wychodzą mi wartość najwieksza w punkcie 2 a ma być 1

salamandra: pokaż

Mila:

	a2
hb=(H2+		)1/2 wpisz H2 obliczone z porównania , jak napisałeś i włącz a
	4

pod pierwiastek . Pamiętaj : a√b=√a²*b wtedy uprościsz wyrażenie

a7: Pole boczne to cztery trójkąty czy tam nie trzeba jeszcze pomnożyć razy 4?

jaros:

	1		32		a2
Hmmm mam czy to Pb = 4*		* √		+		* a
	2		a4		4

jaros: pomoże mi ktoś w leczeniu tutaj pochodnej? jak wstawie a pod pierwiastek to może razy a²?

a7: no tak tylko lepiej chyba zapisać w nawiasie to, co pod pierwiastkiem, żeby było widać o co chodzi

a7: sprowadź chyba do wspólnego mianownika to , co pod pierwiastkiem

salamandra:

	4√2
V=
	3

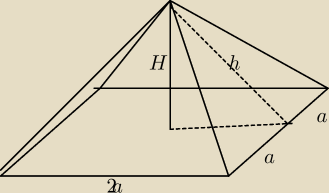
Pp=4a²

	1
V=		*Pp*H
	3

4√2		1
	=		*4a2*H
3		3

4√2=4a²*H

	4√2		√2
H=		=
	4a2		a2

z tw. Pitagorasa H²+a²=h²

2
	+a2=h2
a4

	2+a6
h2=
	a4

	√2+a6
h=
	a2

1		√2+a6   2a*   a2		√2+a6		√2+a6
	Pb=		=a*		=
4		2		a2		a

a7:

	128+a6
√(		)
	a2

a7: bardzo ładny pierwiastek

salamandra:

	√2+a6
nie wiem niestety jak wyznaczyć pochodną z
	a

Szkolniak:

d		√a6+2		6a5   a* −√a6+2   2√a6+2
	(		)=		=...
dx		a		a2

jaros: Ok mam już to co chciałem otrzymać otóż badamy funkcje pod pierwiastkiem (włączyłem już a), ponieważ funkcja pierwiastkowa jest rosnąca (mógłby mi ktoś napisać dokładnie jak mam to opisać?) przyjmuje te same ekstrema co funkcja pierwiastkowa więc:

	32		a4
f(a) =		+
	a2		4

	−64
f'(a) =		+ a3 ====> (policzyłem pochodzie 2 wyrażeń)
	a3

Sprawdzam czy występują miejsca zerowe:

−64
	+ a3 = 0
a3

a⁶ = 64. I pierwiaskuje (pierwiastek 2 stopnia) a³ = 8 v a³ = −8 a = 2 v a = −2 I teraz takie pytanie, , czy trzeba tutaj wyliczyć dziedzinę dla wyrażenia pod pierwiastkiem?

	−64
oraz jak napisać czy funkcja		+ a3 = 0 zmienia znak w −2 i 2 ?
	a3

a7: no to w końcu z czego mamy liczyć pochodną? myślałam, że z całego pola bocznego

Szkolniak:

	d
Tfu, oczywiście pewnie		, używając takiego zapisu.
	da

jaros: No liczymy pochodną z pola bocznego, tak jak napisałem, funkcja optymalizowana jest prawidłowa teraz musze rozwiązać problem (bo nie wiem jak narysować wykres do tego, gdzie pochodna zmienia znak a gdzie nie).

jaros: Czy porostu machnąć wykres wielomiany od góry?

salamandra: @a7 nie ma to znaczenia, czy obliczymy ekstrema dla jednej czy dla czterech

salamandra: @jaros zbierz to wszystko do kupy, bo ja nawet nie widzę skąd u Ciebie w f(a) te wartości

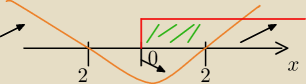
jaros: Zatem funkcje przyjmuje maks w a = 2

jaros:

	1		32		a2
@salamandra no patrz mamy wzór na Pb = 4 *		* √ (		+		) * a
	2		a4		4

Włączam a pod pierwiastkiem i stąd masz funkcje f(a), potem pochodną obliczem z wzoru na pochodną ilorazu i tyle

jaros: i teraz pytanie jaka jest dziedzina do zadania, ktoś mi podpowie bo to też jest punktowane na maturze, normalnie napisał bym a ∊ (0,+∞) ale dość skomplikowane to zadanie i nie wiem czy czegoś nie przeoczyłem

a7: czy ta funkcja ie powinna zmieniać znaku z plusa na minus?

a7: ta pochodna

a7: w sensie, żeby to było maksimum?

salamandra: Jeśli powinno wyjść max dla a=1, to moje rozwiazanie jest ok

salamandra: Albo i nie, poddaje się na dziś, rano spróbuje jak nie dasz rady zrobić

a7: moim zdaniem trzeba całą pochodną liczyć z pierwiastka i przyrównywać do zera to, co będzie w liczniku wtedy będziemy wiedzieli, co tam się dzieje, zaraz spróbuję policzyć

jaros: Dobra rozwiązałem, zaraz napisze rozwiązanie "dla potomnych"

Szkolniak:

	4√2		a2*H		4√2		32
(V=		∧ V=		) ⇒ H=		⇒ H2=
	3		3		a2		a4

Wyliczam h_b:

	a2		a6+128		√a6+128
H2+		=hb2 ⇒ hb=√		⇔ hb=
	4		4a4		2a2

Podstawiam do wzoru na P_b:

	√a6+128		√a6+128
Pb=2*a*hb=2*a*		=
	2a2		a

Tworzę funkcję P(a):

	√a6+128
P(a)=		, a∊(0;+∞) (Co do dziedziny również nie jestem pewien)
	a

	2(a6−64)
P'(a)=
	a2*√a6+128

P'(a)=0 ⇔ a⁶−64=0 a⁶−64=0 (a³−8)(a³+8)=0 (a−2)(a²+2a+4)(a+2)(a²−2a+4)=0 (dzielimy przez dwumiany kwadratowe, bo Δ<0) (a+2)(a−2)=0 . . . Ja bym zrobił w ten sposób, ale u mnie maximum lokalne przyjmowane jest w punkcie a=−2, więc pytanie czy gdzieś mam błąd czy jednak szukamy minimum a nie maksimum.

a7: Ok

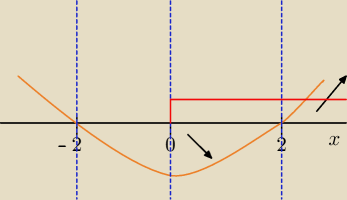
jaros: Więc tak znaleźliśmy funkcje optymalizowaną, która jest podana wyżej. 1) Wyznaczamy dziedzinę: a>0 ===> boki nie mogą być ujemne

	32
a ∊ R − {0} ===>		= {a4}{4} ≥ 0, część wspólna to a ∊ (0;+∞) 1 pkt.
	a2

2) Wzór funkcji optymalizowanej 2 pkt.

	−64
3) Obliczenie pochodnej 1 pkt. f'(a) =		+ a3 1 pkt.
	x3

4) Obliczenie miejsc zerowych a = 2 v a = −2 1 pkt. 5) a∊(0;2): pochodna maleje a∊(2;+∞) pochodna rośnie Zatem dla argumentu a = 2 funkcja w podanej dziedzinie przyjmuje wartość najmniejszą. 1 pkt.

	1
6) Pb = 4 *		* √12
	2

P_b = 2 * √2*2*3 P_b = 4√3 1 pkt 7 pkt. ============ KONIEC! XD ale się tutaj namyśliłem

jaros: Jak coś to w poleceniu mam błąd i chodzi o najmniejsze możliwe pole

a7: no właśnie się dziwowałam

Szkolniak: No i darmowe 7pkt na maturze jaros

jaros: Jak już wiem jak walczyć z takim zadaniem optymalizowanym to jest łatwo, chociaż te zadania są bardzo niesprawiedliwe, bo wystarczy, że nie znajdziesz funkcji, która masz optymalizować i 14% papa

Szkolniak: Racja, ale moim zdaniem zadania optymalizacyjne odnośnie graniastosłupów, ostrosłupów itd są bardzo schematyczne i chyba można powiedzieć że robi się w każdym to samo. Ale jak dla mnie zadania z geometrii za 3/4 punkty o wiele trudniejsze niż te za 7..