Twierdzenie sinusów Dale Cooper: Cześć, pojawił mi się problem w następującym zadaniu: Wykaż, że jeśli a, b, c oznaczają długości boków trójkąta, przy czym a<b<c, i miary kątów tego trójkąta tworzą ciąg arytmetyczny o różnicy 45st., to a/b+c/b=√2. Obliczyłem już kąty (15, 60, 105) Obliczyłem sin15 oraz sin 105 i teraz próbuję zastosować twierdzenie sinusów, ale wychodzą mi jakieś zupełnie bez sensu wyniki. Ktoś pomoże?

Szkolniak:

sin15o		sin105o		sin15o+sin105o
	+		=		=... w liczniku wzór na
sin60o		sin60o		sin60o

sumę sinusów

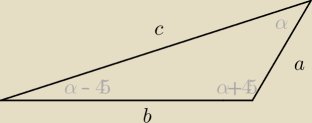
Saizou : 180=3α α=60 , zatem mamy kąty 15, 60, 105

a
	=2R
sin15

a=2Rsin15 (podobnie) b=2Rsin60 c=2Rsin105

a		c		sin15		sin105
	+		=		+		=
b		b		sin60		sin60

	1		√6−√2		√6+√2		2		√6
		(		+		)=		*		=√2
	√3   2		4		4		√3		2

Dale Cooper: Dzięki. Rysunek zrobiłem zupełnie nie taki i mi to trochę zniekształciło obraz, teraz wszystko łapię.

Saizou : Pamiętaj: Największy kąt leży naprzeciw najdłuższego boku, a najmniejszy naprzeciwko najkrótszego boku.

Dale Cooper: Dzięki, będę pamiętał