kwadrat michał: Wewnątrz kwadratu ABCD wybrano punkt M, tak,że |BM| : |AM| : |DM|=1:2:3 Wyznacz miarę kąta AMB

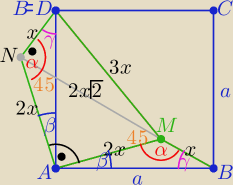
Eta: Można tak: Obrót punktu B o 90^o wokół punktu A ( jest izometrią ) zatem ΔAMB≡ ΔAND to ΔNAM jest prostokątny i równoramienny o ramionach długości 2x więc |∡ANM|=|∡AMN45^o i |MN|=2x√2 Sprawdzamy jakim trójkątem jest ΔDMN z tw. odwrotnego do tw. Pitagorasa x²+(2x√2)² = x²+8x² = (3x)² zatem ΔDNM jest prostokątny i |∡DNM|=90^o to α= 45^o+90^o |∡AMB|=α=135^o ============