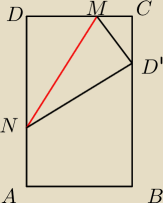
 Prostokatna kartke o wymiarach |AB| = a, |AD| = b (a < b) zagieto tak jak na rysunku.
Wyznacz punkty M tak, aby slad zgiecia MN byl najkrotszy.
Prostokatna kartke o wymiarach |AB| = a, |AD| = b (a < b) zagieto tak jak na rysunku.
Wyznacz punkty M tak, aby slad zgiecia MN byl najkrotszy.
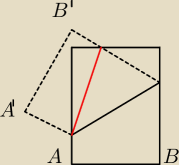 W sensie tak zginana jest kartka ,,, tak
W sensie tak zginana jest kartka ,,, tak  I szukamy minimum dla |NM|
I szukamy minimum dla |NM| 
 Polecenie przpisane 1 do 1, nic wiecej nie ma
Polecenie przpisane 1 do 1, nic wiecej nie ma
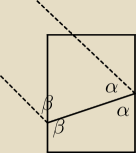 Więc przyjmuję że właśnie oto chodzi.
Zauważ, że linia zgięcia ND' wyznaczam nam trapez ABD'N o kąta α i β
Po zgięciu musimy dostać przystający trapez A'B'D'N, więc mamy także kąty α i β
(β zaznaczony tylko obrazowo −−− w zadaniu jest zbyteczny)
Więc przyjmuję że właśnie oto chodzi.
Zauważ, że linia zgięcia ND' wyznaczam nam trapez ABD'N o kąta α i β
Po zgięciu musimy dostać przystający trapez A'B'D'N, więc mamy także kąty α i β
(β zaznaczony tylko obrazowo −−− w zadaniu jest zbyteczny)

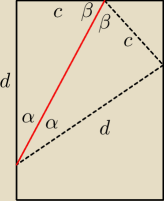 jeszcze raz rysunek:
to lewy górny róg kartki zginamy 'do doły'
jeszcze raz rysunek:
to lewy górny róg kartki zginamy 'do doły'
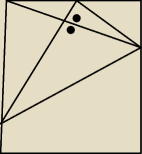 mamy cos takiego
mamy cos takiego
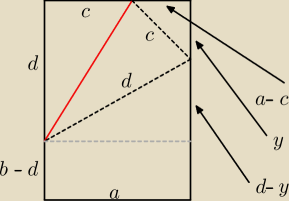
| e*f | ||
Pdeltoidu = | ... chcemy znaleźć minimalne f. | |
| 2 |
| a2 + y2 | ||
c2 = (a−c)2 + y2 −−−> 2ac = a2 + y2 −−> c = | ||
| 2a |
| a2 + y2 | ||
d2 = a2 + (d−y)2 −−−> 2yd = a2 + y2 −−> d = | ||
| 2y |
| a2 + y2 | a2 + y2 | |||
no to mamy f(y) = ( ( | )2 + ( | )2 )1/2 | ||
| 2a | 2y |
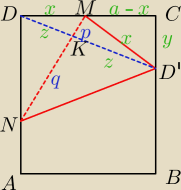 Trojkat MCD'
y2 = x2 − (a − x)2 ===> y2 = 2ax − a2
Trojkat DCD'
Trojkat MCD'
y2 = x2 − (a − x)2 ===> y2 = 2ax − a2
Trojkat DCD'
| ax | ||
(2z)2 = a2 + 2ax − a2 ===> z = √ | ||
| 2 |
| ax | 2x2 − ax | |||
p2 = x2 = | ===> p = √ | |||
| 2 | 2 |
| ax | 2x2 − ax | ax | ||||||||||||
= q * √ | ===> q = | |||||||||||||
| 2 | 2 |
|
| 2x2 − ax | ax | ||||||||||||
|MN| = p + q = √ | + | = | |||||||||||
| 2 |
|
| 2x2 | |||||||||||||||||||||
= | = | = | ||||||||||||||||||||
|
|
| 4x4 | ||
√ | ||
| 4x2 − 2ax |
| 4x4 | ||
f(x) = | ||
| 4x2 − 2ax |
| 16x3(4x2 − 2ax) − 4x4(8x − 2a) | ||
f'(x) = | = | |
| (4x2 − 2ax)2 |
| 32x5 − 24ax4 | ||
= | ||
| (4x2 − 2ax)2 |
| 3 | ||
f'(x) = 0 <=> 32x5 − 24ax4 = 0 <=> 8x4(4x − 3a) <=> x = 0 v x = | a | |
| 4 |
| 3 | ||
f'(x) < 0 <=> x ∊ (0, | a) | |
| 4 |
| 3 | ||
f'(x) > 0 <=> x ∊ ( | a, a> | |
| 4 |
| 3 | ||
Finalnie Punkt M bedzie znajdowac sie w odleglosci | a od wierzcholka D | |
| 4 |
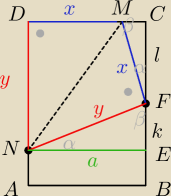 Trochę łatwiejsze rachunki
Trochę łatwiejsze rachunki  MN2=x2+y2
ΔNEF ~ ΔFCM (kkk)
MN2=x2+y2
ΔNEF ~ ΔFCM (kkk)
| a | l | ax | |||
= | ⇒ l= | ||||
| y | x | y |
| k | a−x | y(a−x) | |||
= | ⇒ k= | ||||
| y | x | x |
| ax | y(a−x) | |||
y= | + | |||
| y | x |
| ax2 | ||
y2= | ||
| 2x−a |
| ax2 | 2x3 | |||
MN2=x2+ | = | = f(x) | ||
| 2x−a | 2x−a |
| 6x2(2x−a)−2x3*2 | ||
f'(x)= | =0 | |
| (2x−a)2 |
| 3 | ||
x= | a <−− sprawdzić czy faktycznie jest minimum | |
| 4 |