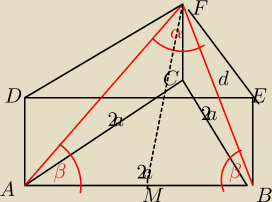
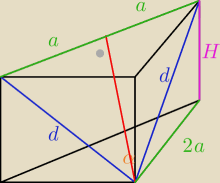
stereometria salamandra: Objętość graniastosłupa prawidłowego trójkątnego jest równa 8, a przekątne dwóch ścian bocznych poprowadzone z jednego wierzchołka tworzą kąt α . Oblicz długość krawędzi podstawy tego graniastosłupa. 1 sposób) w ΔMBF

	α		a
sin		=
	2		d

	α
d*sin		=a
	2

	a
d=
	α   sin   2

w ΔBCF (2a)²+H²=d²

	a2
4a2+H2=
	α   sin2( )   2

	a2
H2=		−4a2
	α   sin2( )   2

	α   a2−4a2(sin2( ))   2
H2=
	α   sin2( )   2

	α   a2(1−4sin2( ))   2
H2=
	α   sin2( )   2

	α   a√1−4sin2( )   2
H=
	α   sin   2

2 sposób z tw. sinusów 2β+α=180

	α
β=90−
	2

d		2a
	=
α   cos   2		sinα

	α
d*sinα=2a*cos
	2

	α   2a*cos   2		a
d=		=
	α   α   2sin *cos   2   2		α   sin   2

I nie wiem którą drogą iść, czy to "H" jest "dobrze" wyznaczone i teraz wstawiać do V, czy w ogóle inaczej do tego podejść?

wredulus_pospolitus:

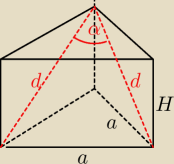
	a2H√3		32√3
V =		= 8 −−> a2 =
	4		3H

d² = a² + H² a² = 2d²(1 − sinα) −> a² = 2(a²+H²)(1−sinα) −−> a²(2sinα − 1) = 2H²(1−sinα) −−−>

	1−sinα		32√3		1−sinα
−−−> a2 = 2H2		−−−>		= 2H2
	2sinα − 1		3H		2sinα − 1

wyznaczasz 'okropną' postać H

wredulus_pospolitus: tfu ... oczywiście nie sinα tylko cosα wszędzie jest (jeszcze chyba śpię )

salamandra: to to co zrobiłem to jest źle?, ta moja "postać" H?

wredulus_pospolitus: I sposób −−− H jest dobrze wyznaczone. Warto napisać na początku założenie: α ∊ (0 ; π/3) Co później pozwala nam ze spokojem stwierdzić, że 1 − 4sin²(α/2) ≥ 0

wredulus_pospolitus: Właśnie poczułem dziwne "deja vu" II sposób całkowicie zbyteczny ... te przekształcenia były po to by wyznaczyć 'd' które wcześniej wyznaczyłeś w jednej linijce.

salamandra: Myślałem, że może jakoś trzeba tym "drugim sposobem" kontynuować po tym jak zobaczyłem jaka postać "H" mi wyszła. To, że α nalezy do takiego przedziału to wynika stricte z tego pierwiastka?

wredulus_pospolitus: Nie ... to że α należy do tego przedziału wynika z tego jaki jest kąt w podstawie graniastosłupa.

salamandra: a nie są to dwa niezależne od siebie kąty? rozumiem poniekąd o co Ci chodzi, ale nie umiem sobie tego zobrazować, bo kąt α nie jest kątem płaskim

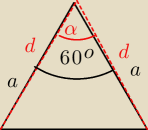
wredulus_pospolitus: widok 'z góry' na graniastosłup

salamandra: W każdym razie mam V=8

	4a2√3
Pp=		=a2√3
	4

	α   a√1−4sin2( )   2
8=a2√3*
	α   sin   2

	α   a3√(3(1−4sin2( )   2
8=
	α   sin   2

I tutaj jest troche kosmos

wredulus_pospolitus: wyobraź sobie sytuację jaki będzie kąt α jeżeli H = 0.00000000000000000000000000000001 a jaka będzie jak jeszcze zmniejszać będziemy to H do 0. Kąt α będzie coraz bliżej wartości 60^o (ale nigdy jej nie osiągnie). Z kolei jeżeli będziemy zwiększać H .... H = 10^100000000000 to przy stałym 'a' (powiedzmy a=1) tenże kąt α będzie coraz to mniejszy i mniejszy, ale nigdy nie będzie równy 0^o

wredulus_pospolitus: No kosmos ... tam gdzie ja zacząłem H wyznaczać (poza oczywistym błędem −−− pisałem sinα zamiast cosα) także kosmos wychodził

salamandra: Teraz czaję

an: >>bo kąt α nie jest kątem płaskim<< czyli jaki jest, mógłbyś mnie oświecić

salamandra: mając wyznaczone "d" z tw. cosinusów w ABF również kosmos:

	2a2		2a2
4a2=		−		*cosα
	α   sin2( )   2		α   sin2( )   2

α   4a2(sin2( )−2a2   2		2a2
	=−		*cosα
α   sin2( )   2		α   sin2( )   2

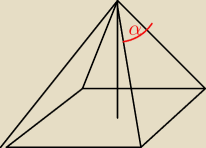
salamandra: @an, nie wiem, z określeniem "kąt płaski" spotykałem się, gdy kąt był po prostu na którejś ścianie, a nie w bryle. np taki:

an: Kąt płaski jest to kąt na płaszczyźnie, dwie proste przecinające się lub równoległe, wyznaczają płaszczyznę. Kąt α wyznaczony jest przez przecinające się proste zawierające przekątne ścian bocznych jak pisze w zadaniu, a więc muszą znajdować się na jednej płaszczyźnie (wraz z tym kątem który tworzą) wikipedia Kąt – obszar powstały z rozcięcia płaszczyzny przez sumę dwóch różnych półprostych o wspólnym początku, wraz z tymi półprostymi[1]. Półproste nazywane są ramionami kąta, wspólny początek półprostych nazywany jest wierzchołkiem kąta. Obszar ten bez wspomnianych półprostych, tj. jego wnętrze, nazywa się niekiedy kątem otwartym (por. zbiór otwarty), opatrując dla kontrastu pierwotną definicję nazwą kąta domkniętego (por. zbiór domknięty). Kąt można też zdefiniować jako część wspólną lub jako sumę dwóch półpłaszczyzn z brzegiem wyznaczonych przez dwie nierównoległe proste. Wówczas należy dodatkowo zdefiniować „kąt pełny” jako całą płaszczyznę, „kąt półpełny” jako półpłaszczyznę oraz „kąt zerowy” jako półprostą. Gdy kąt obejmuje całą płaszczyznę (w przypadku „kąta pełnego”) pomocne bywa wyróżnienie na płaszczyźnie półprostej pełniącej rolę ramion i z jej początkiem jako wierzchołkiem kąta. Podobnie gdy ramiona dopełniają się do prostej (dając „kąt półpełny”) wyróżnia się czasem wspólny początek półprostych, tj. ustalony punkt powstałej prostej, jako wierzchołek.

salamandra: dzięki za wyjaśnienie

Saizou :

	α		a		a
sin		=		→d=
	2		d		α   sin   2

d²=H²+4a²

a2		α		α		1−cosα
	=H2+4a2 1−cosα=2sin2		→sin2		=
α   sin2   2		2		2		2

2a2
	=H2+4a2
1−cosα

	1
H2=2a2(		−2)
	1−cosα

	2cosα−1
H2=2a2*
	1−cosα

8=P_p*H 64=P_p²*H²

	4a2√3		2cosα−1
64 = [		]2 * 2a2*
	4		1−cosα

	2cosα−1
64 = 6a6*
	1−cosα

	32(1−cosα)
a6=
	3(2cosα−1)

	32(1−cosα)
a=6√
	3(2cosα−1)

wredulus_pospolitus: Ogólnie −−− to zadanie bardziej przypomina zadania 'ze starych czasów' (patrz −−−moja matura) niż to co jest na nowej maturze

Saizou : wg mnie nawet dobrze, że tak się dzieje. NIech ćwiczą sprawność rachunkową.

Mila: 2a − krawędź podstawy

	α
1) Obliczyć wysokość przekroju: h=a*ctg
	2

2) Wysokość gran.

	a√3
h2=(		)2+H2
	2

3) Podstawić do wzoru 8=a²√3*H