Nie wiem jak to zrobić a potrzebuje na jutro rano
Luki: Na ile różnych sposobów można pomalować krawędzie nieoznaczonego
sześcianu mając do dyspozycji cztery kolory tak aby dwie spośród nich miały przyporządkowany
kolor czerwony, dwie zielony, cztery kolor niebieski i reszta była w kolorze żółtym.
Nie wiem jak to zrobić a potrzebuje na jutro rano jest to zagadnienie z Kombinatorycznych
podstaw informatyki. Będę wdzięczny za każdą pomoc.
26 kwi 21:40
Godzio:
| |
−− malujemy na czerwono 2 krawędzie. |
| |
| |
−− dwie kolejny na zielono (z tych, które pozostały) |
| |
| |
= 1 −− pozostałe na żółto |
| |
Wymnóż wszystko, a otrzymasz wynik.
26 kwi 21:52
Luki: właśnie jak ostatnie przedstawiłem taki wynik to prowadząca poinformowała mnie że to złe
podejście dlatego właśnie nie wiem jak to zrobić
26 kwi 21:59
wredulus_pospolitus:
Podejście dobre ale ... faktycznie nie jest to prawidłowe podejście do tego zadania ponieważ
tak licząc niestety liczymy parokrotnie tak samo pomalowane sześciany.
Należy zauważyć, że sześcian jest NIEOZNACZONY

(czyt. krawędzie nie są rozróżnialne).
Analogiczne zadania są z siadaniem przy okrągłym stole (gdzie krzesła nie są numerowane).
26 kwi 22:04
Godzio: Macie racje, mój błąd. Łatwo się nabrać.
26 kwi 22:15
wredulus_pospolitus:
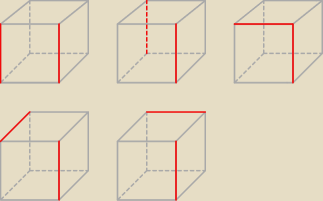
Dlatego winno być:
5 −−− pomalowanie czerwonych
i te czerwone są naszym 'punktem odniesienia' do dalszego malowania (krawędzie pomimo
niepodpisania wierzchołków stają się 'rozróżnialne' względem ich pozycji do czerwonych
krawędzi)
więc dalej mamy:
Na rysunku przedstawiłem różne możliwości pomalowania na czerwono, które są od siebie różne
(obracając sześcian nie z np. pozycji (1) nie damy rady tak ułożyć sześcianu aby pokazał np.
pozycję (3) )
Miałem wątpliwość co do (4) i (5) (czy to nie ta sama sytuacja), ale po chwili obracania
kostką do gry stwierdziłem, że chyba jedna nie.
26 kwi 22:35
a7: dwie czerwone krawędzie może wybrać na 5 różnych sposobów, potem zielone na 5 sposobów (?)
potem niebieskie na 4 (?) sposoby i pozostałe 4 na 1 sposób
5*5*4*1=80

26 kwi 22:40
a7:
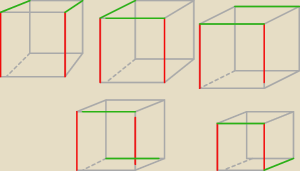
rozmieszczenie zielonych, 5 sposobów, przy jednym sposobie czerwonych
26 kwi 22:46
a7:
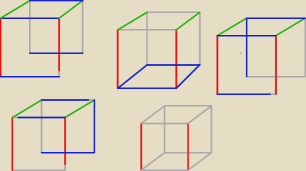
rozmieszczenie niebieskich, 4 sposoby, przy jednym sposobie czerwonych i zielonych
26 kwi 22:50
a7: oczywiście źle pomnożyłam, ale mi wyszło 5*5*4*1=100 (nie 80) jeszcze sprawdzam
26 kwi 22:52
wredulus_pospolitus:
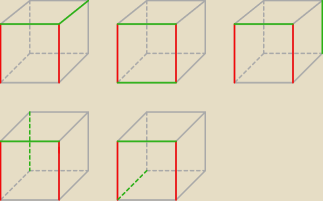
a7 częściowo masz rację, ale:
zabrakło (rysunki)
I może jeszcze jakiś (chociaż chyba wszystkie wykorzystałem)
Teraz tak naprawdę by trzeba było spojrzeć na pozostałe (4) układy czerwonych i też je tam
rozpisać ... w pipe roboty
Przy kolejnym kolorze także np. (2) z moich rysunków trzeba rozpatrywać indywidualnie (bo może
go nadal obrócić o 180
o), reszta już będzie 'wyjątkowa'.
Nie wiem co strzeliło nauczycielowi by dać takie zadanie.
26 kwi 23:00
a7:
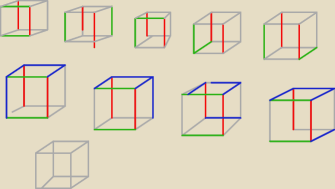
rozmieszczenie zielonych (5 sposobów) dla drugiego rozmieszczenia czerwonych u
Wredulusa
oraz rozmieszczenie
niebieskich (cztery sposoby) dla pierwszego z nich
także chyba jednak odpowiedź to będzie 100

26 kwi 23:02
a7: mi się wszystko zgadza jest 100 sposobów na każdy układ czerwonych przypada pięć układów
zielonych na każy z układów zielonych cztery niebieskie
4*5*5=.......
26 kwi 23:04
a7: chociaż 100% pewności to ja nie mam, ale mogę porysować

26 kwi 23:06
a7: Będziesz sprawdzał?
26 kwi 23:06
wredulus_pospolitus:
a7 −−− ale już na etapie malowania 'zielonym' nie rozpatrzyłaś wszystkich przypadków.
Szczerze −−− nie mam zacięcia do sprawdzania tego dalej (dla malowania na zielono przy innym
układzie czerwonych ... nie wspominając o dalszym malowaniu na niebiesko).
Tak jak napisałem −−− co nauczycielce strzeliło do łba ... no chyba że myślała tak jak ja
początkowo (albo jeszcze prościej −−− że wystarczy wziąć jedną krawędź pomalować na czerwono i
gotowy punkt odniesienia).
26 kwi 23:09
a7: zaraz policzę ile jest tych zielonych, ale czy tych niebieskich jest przynajmniej dobra ilość
sposobów (4 na każdy zielony)
26 kwi 23:13
wredulus_pospolitus:
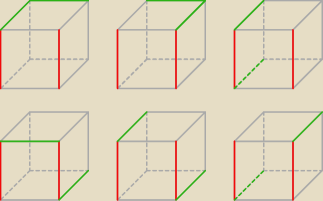
kolejny brakujący do kolekcji z 23:00 itd. już mi się nie chce tych sześcianów rysować

26 kwi 23:18
wredulus_pospolitus:
a7 −−− nie ... nie w każdym będą 4 sposoby ... patrz post (23:00) (2) rysunek ... jego nadal
można obrócić o 180o i dostaniesz ten sam sześcian (przy kolorze czerwony i zielonym) więc to
redukuje możliwości dla koloru niebieskiego
26 kwi 23:20
a7:
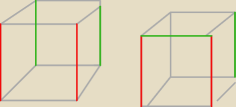
aktualna wersja to
5*12*4=240
26 kwi 23:22
wredulus_pospolitus:
@a7 doceniam Twoje 'zaparcie' w tym zadaniu, ale ja sobie odpuszczam ... bo coś czuję że to
nadal (przy tych dwóch czerwonych 'z przodu') nie są wszystkie możliwości (mówię o tych
wspólnie narysowanych 16 możliwościach) pomalowania na zielono.
26 kwi 23:22
wredulus_pospolitus:
(2) rysunek z 23:22 masz powielony z rysunkiem (3) z godziny 23:00
26 kwi 23:24
wredulus_pospolitus:
A sam autor sobie już dawno to zadanie odpuścił

26 kwi 23:25
a7: nie jest powielony na tym dwie przednie są czerwone i dwie tylnie są zielone,a na drugim
sześcianie górna jest zielone i tylnia po prawej a nie lewej stronie
nie ważne
zobaczymy może ktoś to raz dwa rozkmini, bez liczenia na piechtę
26 kwi 23:30
wredulus_pospolitus:
@a7 −−− post z 23:00 rysunek (3) (pierwszy rząd ... trzeci od lewej) −−− zielona krawędź
górna i 'tylna prawa'
26 kwi 23:32
a7: a faktycznie, ten się zdublował, dobra, już też mam dosyć, przecież już spasowałam,
26 kwi 23:37
Saizou :
Taka wolna myśl:
może się zastanowić ile sześcianów przeliczamy za dużo w wersji Godzia?
26 kwi 23:43
wredulus_pospolitus:
Saizou −−−− niestety ... patrząc na to co później rysowała a7 i ile patrząc nawet później mamy
'dublujące' się układy (nawet przy trzecim kolorze) powiem Ci, że chyba bez przemalowania
wszystkiego nie dojdziemy do tego o ile za dużo.
| | | |
Godzio już na etapie pierwszego koloru mocno przestrzelił co pokazałem bo z | |
| | |
zjechaliśmy do raptem 5
| | | |
Teraz trzeba zobaczyć ile z | trzeba zjechać ... zatrzymaliśmy się obecnie na 17 |
| | |
sztukach (a to pewnie nie są wszystkie) i co gorsza ... nie mamy pewności czy dla innych
układów pomalowania czerwonych krawędzi będzie tyle samo wersji malowań na zielono.
Podsumowując: Tragedia

26 kwi 23:49
a7:
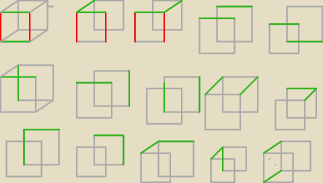
aktualny stan to 5*21*4=404, zaraz dorysuję jeszcze 6 z pierwszego ułożenia czerwonych (c.d.n)
27 kwi 00:18
a7:
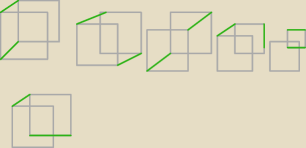
27 kwi 00:18
wredulus_pospolitus:
się jednak nie poddała

27 kwi 00:18
wredulus_pospolitus:
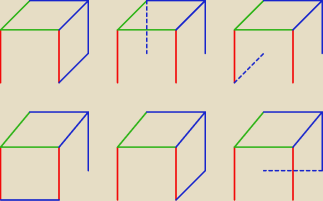
a7 −−− wybacz, ale to nadal nie będzie ok co piszesz, bo np. dla większości sześcianów będzie
już jednoznaczny, więc niebieski kolor dla nich (np. dla (2) z 00:18) będzie można malować
| | | |
niebieski na | = 14 sposobów (narysowałem tylko 6 ... ale mam nadzieję że rozumiesz o |
| | |
co mi chodzi)
27 kwi 00:30
a7: no to aktualny stan 5*21*14*1=
1470 (liczone na kalkulatorze)

27 kwi 00:34
27 kwi 00:36
wredulus_pospolitus:
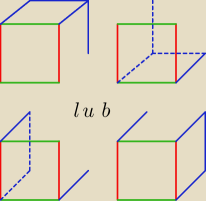
nie a7 ... bo z kolei masz inne takie jak np. (1) z 00:18 które możesz obrócić o 180
o i
otrzymasz ten sam sześcian, więc pozycje niebieskiego takie jak na rysunku się dublują
(oczywiście jest więcej taki par)
27 kwi 00:39
wredulus_pospolitus:
| | | |
no i oczywiście | = 70  |
| | |
27 kwi 00:41
a7: 
Dobrej , spokojnej nocy

27 kwi 00:43
 (czyt. krawędzie nie są rozróżnialne).
Analogiczne zadania są z siadaniem przy okrągłym stole (gdzie krzesła nie są numerowane).
(czyt. krawędzie nie są rozróżnialne).
Analogiczne zadania są z siadaniem przy okrągłym stole (gdzie krzesła nie są numerowane).
 Dlatego winno być:
5 −−− pomalowanie czerwonych
i te czerwone są naszym 'punktem odniesienia' do dalszego malowania (krawędzie pomimo
niepodpisania wierzchołków stają się 'rozróżnialne' względem ich pozycji do czerwonych
krawędzi)
więc dalej mamy:
Dlatego winno być:
5 −−− pomalowanie czerwonych
i te czerwone są naszym 'punktem odniesienia' do dalszego malowania (krawędzie pomimo
niepodpisania wierzchołków stają się 'rozróżnialne' względem ich pozycji do czerwonych
krawędzi)
więc dalej mamy:

 rozmieszczenie zielonych, 5 sposobów, przy jednym sposobie czerwonych
rozmieszczenie zielonych, 5 sposobów, przy jednym sposobie czerwonych
 rozmieszczenie niebieskich, 4 sposoby, przy jednym sposobie czerwonych i zielonych
rozmieszczenie niebieskich, 4 sposoby, przy jednym sposobie czerwonych i zielonych
 a7 częściowo masz rację, ale:
zabrakło (rysunki)
I może jeszcze jakiś (chociaż chyba wszystkie wykorzystałem)
Teraz tak naprawdę by trzeba było spojrzeć na pozostałe (4) układy czerwonych i też je tam
rozpisać ... w pipe roboty
Przy kolejnym kolorze także np. (2) z moich rysunków trzeba rozpatrywać indywidualnie (bo może
go nadal obrócić o 180o), reszta już będzie 'wyjątkowa'.
Nie wiem co strzeliło nauczycielowi by dać takie zadanie.
a7 częściowo masz rację, ale:
zabrakło (rysunki)
I może jeszcze jakiś (chociaż chyba wszystkie wykorzystałem)
Teraz tak naprawdę by trzeba było spojrzeć na pozostałe (4) układy czerwonych i też je tam
rozpisać ... w pipe roboty
Przy kolejnym kolorze także np. (2) z moich rysunków trzeba rozpatrywać indywidualnie (bo może
go nadal obrócić o 180o), reszta już będzie 'wyjątkowa'.
Nie wiem co strzeliło nauczycielowi by dać takie zadanie.
 rozmieszczenie zielonych (5 sposobów) dla drugiego rozmieszczenia czerwonych u Wredulusa
oraz rozmieszczenie
niebieskich (cztery sposoby) dla pierwszego z nich
także chyba jednak odpowiedź to będzie 100
rozmieszczenie zielonych (5 sposobów) dla drugiego rozmieszczenia czerwonych u Wredulusa
oraz rozmieszczenie
niebieskich (cztery sposoby) dla pierwszego z nich
także chyba jednak odpowiedź to będzie 100 

 kolejny brakujący do kolekcji z 23:00 itd. już mi się nie chce tych sześcianów rysować
kolejny brakujący do kolekcji z 23:00 itd. już mi się nie chce tych sześcianów rysować 
 aktualna wersja to
5*12*4=240
aktualna wersja to
5*12*4=240


 aktualny stan to 5*21*4=404, zaraz dorysuję jeszcze 6 z pierwszego ułożenia czerwonych (c.d.n)
aktualny stan to 5*21*4=404, zaraz dorysuję jeszcze 6 z pierwszego ułożenia czerwonych (c.d.n)


 a7 −−− wybacz, ale to nadal nie będzie ok co piszesz, bo np. dla większości sześcianów będzie
już jednoznaczny, więc niebieski kolor dla nich (np. dla (2) z 00:18) będzie można malować
a7 −−− wybacz, ale to nadal nie będzie ok co piszesz, bo np. dla większości sześcianów będzie
już jednoznaczny, więc niebieski kolor dla nich (np. dla (2) z 00:18) będzie można malować

 nie a7 ... bo z kolei masz inne takie jak np. (1) z 00:18 które możesz obrócić o 180o i
otrzymasz ten sam sześcian, więc pozycje niebieskiego takie jak na rysunku się dublują
(oczywiście jest więcej taki par)
nie a7 ... bo z kolei masz inne takie jak np. (1) z 00:18 które możesz obrócić o 180o i
otrzymasz ten sam sześcian, więc pozycje niebieskiego takie jak na rysunku się dublują
(oczywiście jest więcej taki par)

 Dobrej , spokojnej nocy
Dobrej , spokojnej nocy 