Wyznaczenie stycznej DisStream: Wyznacz równania wspólnych stycznych do wykresu funkcji f(x)=x²−x+1 i g(x)=1/2x²−x+2 Wiem, ze trzeba to zrobic za pomocą pochodnych jednak nie potrafie ułozyc rownania

Mirek: Wyznacz punkt przeciecia krzywych : x² −x +1= (0,5)x² −x +2 ⇒0,5 x² = 1 ⇒ x= √2 lub x= − √2 A( √2 ; 3−√2 ) lub B( −√2; 3 +√2 ) punkty stycznosci Styczna : y − y_o = f '(x_o )( x− x_o)

DisStream: i co dalej?

Luki: z zadaniem nie pomogę ale kontent na yt masz fajny

f123: @Mirek twoje rozwiazanie jest bledne. Dlaczego zakladamy, ze styczna bedzie styczna do obu tych funkcji w jedynakowym punkcie? Robimy tak: f'(x) = 2x − 1 g'(x) = x − 1 y − f(x₀) = f'(x₀)(x − x₀) y − g(x₀) = g'(x₀)(x − x₀) Porzadkujesz to, i porownujesz ze soba wspolrzynniki przy 'x' oraz wyrazy wolne

Mirek: Bo inaczej nie masz punktow stycznosci , bo skad ? Porownujac wspolczynniki masz dwie styczne rownolegle , a w tresci napisane " wspolne " !

f123: "wspolne" czyli ze zarowno jest styczne do wykkresu funkcji f i g, ale nie w tym samym punkcie

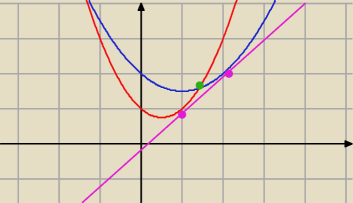
wredulus_pospolitus: Mirek −−− absolutnie nie Pokaż mi jak niby ma wyglądać styczna do obu tych wykresów w punkcie zielonym Na fioletowo zaznaczyłem 'na oko' (nie ma tutaj precyzji − chodzi o pokazanie sytuacji) jedną z tych stycznych. Styczna będzie jedna dla obu tych funkcji, ale funkcje będą miały INNE punkty styczności z tą (jedną) styczną.

Mirek: Napisano w liczbie mnogiej " rownania wspolnych stycznych ! Przez punkt " zielony " przechodzi jedna styczna do jednej krzywej i druga styczna inna do drugiej krzywej

f123: Poprawiajac moje rozwiazanie: y − f(q) = f'(q)(x − q) y − g(p) = g'(p)(x − p)

wredulus_pospolitus: A czy fioletowa nie jest WSPÓLNĄ styczną tych dwóch wykresów No to narysuj mu STYCZNĄ do tych dwóch wykresów w punkcie zielonym (punkt przecięcia się krzywych).

wredulus_pospolitus: Ty dokonałem NADINTERPRETACJI treści zadania zakładając, że ta 'wspólna styczna' musi być styczna w tym samym punkcie do obu krzywych. Takiej stycznej dla tych krzywych NIE BĘDZIE, nie może być.

Mirek: Czyli jest tylko jedna wspolna styczna ?

wredulus_pospolitus: a z tego co piszesz to wnioskuję że w ogóle nie zrozumiałeś treści zadania −−− to ma być WSPÓLNA styczna dla obu krzywych ... a piszesz, że w zielonym punkcie jedna styczna będzie do jednej krzywej a inna (druga) do drugiej krzywej −−−−− czyli masz dwie (różne) styczne ... gdzie tu masz 'wspólne styczne'

wredulus_pospolitus: nie ... druga będzie w II ćwiartce

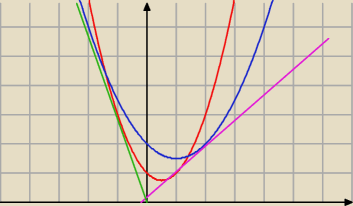
wredulus_pospolitus: UWAGA Styczne narysowane 'na oko' − nie sugerować się rysunkiem w celu odczytania punktów przecięcia się tych stycznych z osiami OX i OY

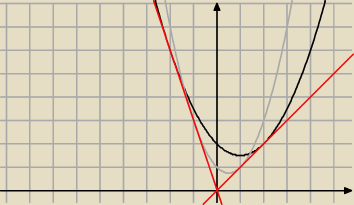
ICSP: y = ax + b styczność z funkcja f: y = ax + b y = x² − x + 1 x² −(1 + a) + 1 − b = 0 Δ = (1 + a)² − 4(1 − b) = 0 styczność z funkcją g: y = ax + b

	1
y =		x2−x + 2
	2

1
	x2 − (1+a) + 2 − b
2

Δ = (1 + a)² − 2(2 − b) = 0 (1 + a)² − 4(1 − b) = 0 (1 + a)² − 2(2 − b) = 0 −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− 4(1−b) = 2(2−b) 4 − 4b = 4 − 2b b = 0 ⇒ a = 1 v a = −3 y = −3x v y = x