pradopodobieństwo jaros: W pierwszej urnie umieszczono n kul białych i 5 kul czarnych, a w drugiej urnie 3 kule białe i n czarnych. Losujemy jedną kulę z pierwszej urny i przekładamy ją do drugiej urny. Następnie losujemy jedną kulę z drugiej urny. Oblicz n, wiedząc, że prawdopodobieństwo wylosowania kuli

	7
białej z drugiej runy jest równe		.
	18

Podpowie mi ktoś co i jak tutaj działaś? Szczerze, pierwszy raz robie zadanie gdzie mam n w liczbach kul i nie wiem jak sobie z tym problemem poradzić.

wredulus_pospolitus: Rozpatrujesz sytuacje: 1) z pierwszej wylosowano białą, z drugiej wylosowano białą 2) z pierwszej wylosowano czarną, z drugiej wylosowano białą

	n		4		5		3		7
P(A) =		*		+		*		=
	n+5		n+4		n+5		n+4		18

rozwiązujesz powyższe równanie

jaros: Czyli zrobić to "drzewkiem"?

a7: jasne w pierwszej urnie mamy na początku n+5 kul prawdopodobieństwo wylosowania białej było

	n
	n+5

	5
prawdopodobieństwo wylosowania czarnej było
	n+5

w drugiej 3+n kul losujemy z pierwszej jedną jeśli to była biała to w drugiej mamy 4+n kul w tym 4 białe jeśli czarna to mamy 4+n kul w tym trzy białe

	7
P(A)=
	18

	n		4		5		3		7
P(A)=		*		+		*		=
	n+5		4+n		n+5		n+4		18

i liczymy

(4n+15)		7
	=
(4+n)(5+n)		18

.................. 7n²−9n−130=0 Δ=3721 √Δ=61 n=5 ===

a7: dzrzewkiem nie trzeba

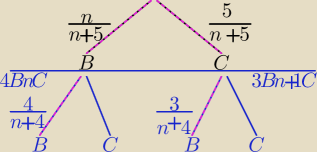
b: nB,5C 3B,nC

n		4		5		3		7
	*		+		*		=
n+5		n+4		n+5		n+4		18

jaros: Dziękuje @a7 oraz @b, wszystko rozumiem @b a tak dla doprecyzowania, niemożliwe jest wyznaczenie tak jakby "ilości czarnych kul" jakimś wyrażaniem z n?

wredulus_pospolitus: nie ... liczba kul czarnych jest Ci znana i jest to konkretna wartość nie mająca żadnego związku z 'n'