czworokat g01: Dany jest czworokąt ABCD taki że AB=AD=1 oraz kąt BAD=90^o. Niech CB=c, CA=b oraz CD=a. Wykaż że (2−a²−c² )²+(2b²−a²−c² )²=4a² c².

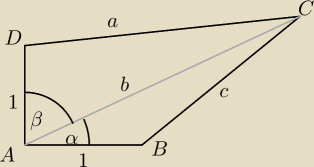
Godzio: β = 90^o − α Najpierw uprośćmy Twoje wyrażenie. 4+a⁴+c⁴+2a²c²−4a²−4c²+4b⁴+a⁴+c⁴−4a²b²−4b²c²+2a²c²=4a²c² 2a⁴+2c⁴+4b⁴−4a²−4c²−4a²b²−4b²c²+4=0 a⁴ + c⁴ + 2b⁴ − 2a² − 2c² − 2a²b² − 2b²c² + 2 = 0 a⁴ − 2a²b² + 2b⁴ + c⁴ − 2b²c² − 2a² − 2c² + 2 = 0 Z twierdzenia cosinusów:

	b2 − a2 + 1
a2 = 1 + b2 − 2bcosβ ⇒ cosβ =		oraz cosβ = sinα
	2b

	b2 − c2 + 1
c2 = 1 + b2 − 2bcosα ⇒ cosα =
	2b

	(b2 − a2 + 1)2
sin2α =
	4b2

	(b2 − c2 + 1)2
cos2α =
	4b2

Dodajemy równania, lewa strona to jedynka trygonometryczna. Mnożę od razu przez 4b². 4b² = (b² − a² + 1)² + (b² − c² + 1)² 4b² = b⁴ + a⁴ + 1 − 2a²b² + 2b² − 2a² + b⁴ + c⁴ + 1 + 2b² − 2c² − 2b²c² 0 = a⁴ − 2a²b² + 2b⁴ + c⁴ − 2b²c² − 2a² − 2c² + 2 Wyszło dokładnie to samo, a zatem mamy koniec.

g01: Dzieki a jak wkonac podpunkt b) Dany jest czworokąt ABCD taki że AB=AD=1 oraz kąt BAD=90^o. Niech CB=c, CA=b oraz CD=a. Wykaż że (a−c)2 ≤ 2b2 ≤ (a+c)2.

g01: Dany jest czworokąt ABCD taki że AB=AD=1 oraz kąt BAD=90^o. Niech CB=c, CA=b oraz CD=a. Wykaż że (a−c)² ≤ 2b² ≤ (a+c)²