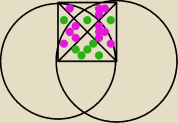
 Dany jest bok kwadratu a. Oblicz sumę pol tych "różowych".
Dany jest bok kwadratu a. Oblicz sumę pol tych "różowych".
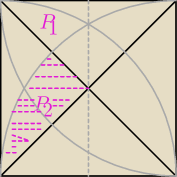
| (πa2−a2) | a2(π−1) | |||
2*P2=2* | = | (pole koła (r=a) minus pole kwadratu na cztery na dwa) | ||
| 8 | 4 |

| πa2−(a√2)2 | a2(π−2) | |||
2P2=2* | = | |||
| 8 | 4 |
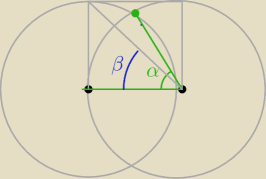 α=60o β=45o γ=α−β=15o
PWYCINKA15o=15/360*π*a2=(1/24)π*a2
α=60o β=45o γ=α−β=15o
PWYCINKA15o=15/360*π*a2=(1/24)π*a2
| a2(π−2) | a2π | |||
P1=2P2−PWYCINKA15o= | − | =........ | ||
| 4 | 24 |
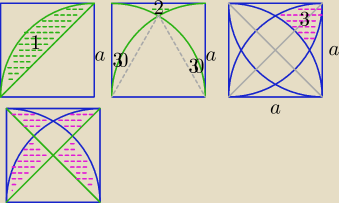
| πa2 | 1 | |||
1) P1= | − | a2− | ||
| 4 | 2 |
| πa2 | a2√3 | a2√3 | πa2 | |||||
P2=a2−( | + | )=a2− | − | |||||
| 6 | 4 | 4 | 6 |
| πa2 | 1 | |||
P3=a2−( | − | a2+2*PΔ)= | ||
| 4 | 2 |
| πa2 | 1 | a2√3 | πa2 | |||||
=a2−( | − | a2+2a2− | − | )= | ||||
| 4 | 2 | 2 | 3 |
| a2√3 | πa2 | a2 | ||||
= | + | − | ||||
| 2 | 12 | 2 |
| πa2 | 1 | a2√3 | πa2 | a2 | ||||||
S=P1+P3= | − | a2+ | + | − | ||||||
| 4 | 2 | 2 | 12 | 2 |
| a2√3 | πa2 | |||
S= | + | −a2 | ||
| 2 | 3 |
| πa2 | ||
P3=a2−( | +2*PΔ∼)= | |
| 4 |
| πa2 | πa2 | a2√3 | ||||
=a2−( | +2a2− | − | ) | |||
| 4 | 3 | 2 |
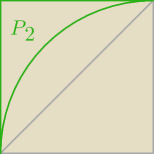 Dobry wieczór Milu nie umiem się zorientować w Twoich obliczeniach, tj. który to jest
trójkąt krzywoliniowy
z punktu 2) myślałam że to ten w rogu P2?
Dobry wieczór Milu nie umiem się zorientować w Twoich obliczeniach, tj. który to jest
trójkąt krzywoliniowy
z punktu 2) myślałam że to ten w rogu P2?
| πa2 | ||
wtedy P2=a2− | atam jest π/6*a2 | |
| 4 |
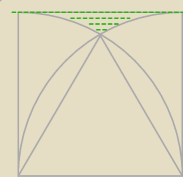 nie rozumiem jak obliczyć P2
nie rozumiem jak obliczyć P2
| a2π | a2√3 | |||
czy tam nie powinno być P−2= a2−2* | − | ? | ||
| 6 | 4 |
| 60 | πa2 | |||
Pw= | *πa2= | |||
| 360 | 6 |
| π | ||
W P2 połączyłam dwa wycinki o kącie | w jeden o kącie U{π}[3}=600. | |
| 6 |
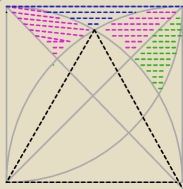 Pole niebieskie równe P2 jest równe polu kwadratu minus dwa wycinki koła 30o minus trójkąt
równoboczny o boku a
Pole niebieskie równe P2 jest równe polu kwadratu minus dwa wycinki koła 30o minus trójkąt
równoboczny o boku a
| a2π | ||
P2=a2−2* | −Ua2√3}{4} | |
| 6 |
| a2π | a2π | a2√3 | 5a3π | |||||
P3=a2− | −2*(a2−2* | −Ua2√3}{4})= | + | −a2 | ||||
| 4 | 6 | 2 | 12 |
| a2π | a2√3 | 5a2π | ||||
S= | −1/2*a2+ | + | −a2 | |||
| 4 | 2 | 12 |
| 3 | 3 | a2√3 | ||||
S= | a2π− | a2+ | ||||
| 4 | 2 | 2 |

| a2√3 | πa2 | 3a2 | ||||
S= | + | − | ≈0.4a2 | |||
| 2 | 3 | 2 |
| a2√3 | 3a2 | a2π | ||||
S= | − | + | ||||
| 2 | 2 | 3 |
| 3√3−9+2π | ||
S=a2 | ||
| 6 |


