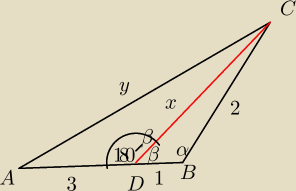
Na boku AB trójkąta ABC wybrano punkt D w ten sposób, że AD=3BD=3. Bok BC tego trójkąta ma
długość 2. Oblicz stosunek długości odcinków AC i DC.
w ΔDBC
x2=4+1−2*cosα
x2=5−2*cosα
4=x2+1−2x*cosβ
wΔABC
y2=20−16*cosα
w ΔADC
y2=x2+9−6x*(−cosβ)
Mogę z tego coś zrobić, czy w ogóle inaczej powinienem podejść do tego zadania?
| y2 | 20−8cosα | ||
= | =... | ||
| x2 | 5−2cosα |
