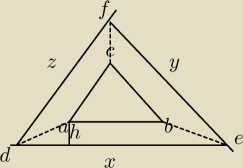
 Każdą z prostych zawierających boki pewnego trójkąta przesunięto w kierunku na zewnątrz
trójkąta o tę samą odległość h, otrzymując trzy nowe proste tworzące większy trójkąt.
Znajdź jego pole i obwód, mając dane pole i obwód wyjściowego trójkąta.
Oznaczyłam boki mniejszego trójkąta ABC przez a,b,c. Przyjęłam,że PABC=P , ObABC=a+b+c
Obliczam kolejno pola trzech trapezów:
PDEBA= (a+x)*h2, PFEBC=(b+y)*h2, PFCAD=(c+z)*h2
Jednak dalej nie wiem co z tym zrobić, czy w ogóle od tego zacząć
Każdą z prostych zawierających boki pewnego trójkąta przesunięto w kierunku na zewnątrz
trójkąta o tę samą odległość h, otrzymując trzy nowe proste tworzące większy trójkąt.
Znajdź jego pole i obwód, mając dane pole i obwód wyjściowego trójkąta.
Oznaczyłam boki mniejszego trójkąta ABC przez a,b,c. Przyjęłam,że PABC=P , ObABC=a+b+c
Obliczam kolejno pola trzech trapezów:
PDEBA= (a+x)*h2, PFEBC=(b+y)*h2, PFCAD=(c+z)*h2
Jednak dalej nie wiem co z tym zrobić, czy w ogóle od tego zacząć 
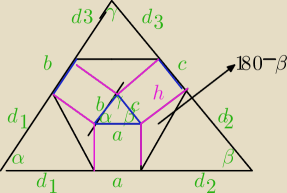 PΔDEF=PΔABC+a*h+b*h+c*h+1/2*h2(sinα+sinβ+sinγ)+1/2(d1)2sinα+1/2(d2)2sinβ+1/2(d3)3sinγ
teraz
P=1/2absinα=1/2bcsinβ=1/2acsinγ sinα= sinβ= sinγ=
z tw. cosinusów cosα= cosβ= cosγ=
PΔDEF=PΔABC+a*h+b*h+c*h+1/2*h2(sinα+sinβ+sinγ)+1/2(d1)2sinα+1/2(d2)2sinβ+1/2(d3)3sinγ
teraz
P=1/2absinα=1/2bcsinβ=1/2acsinγ sinα= sinβ= sinγ=
z tw. cosinusów cosα= cosβ= cosγ=
| h | h | h | ||||
i teraz d1= | d1=..... d2= | d2= d3= | ||||
| tgα2 | tgβ2 | tgγ2 |
| 2P | 2P | 2P | ||||
PΔDEF=P+h(a+b+c)+1/2h2( | + | + | )+1/2*((abh)/2P)2*(2P)/ab+ | |||
| ab | bc | ac |