geometria q2: Dany jest trójkąt ABC, oraz romb ADEF taki, że D, E, F leżą odpowiednio na AB, BC, CA. Wykazać, że pole ADEF jest mniejsze niż połowa pola ABC.

wredulus_pospolitus: ABC jest DOWOLNYM trójkątem

q2: Tak

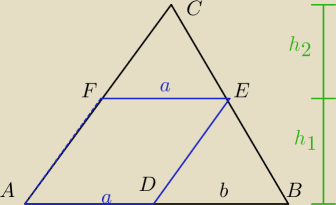
wredulus_pospolitus: patrz na rysunek, zauważ podobieństwo trójkątów CFE i EDB oraz CAB. Skorzystaj z tego

wredulus_pospolitus: Łatwo wykazać, że pole tego rombu MOŻE być równe połowie pola trójkąta ABC

q2: Widzę to podobieństwo ale jak to wykorzystać do pola to nie wiem

wredulus_pospolitus: Wiemy, ze:

a		h2
	=
b		h1

Niech:

a
	= k (k≠0), czyli a = b*k (oraz h2 = h1*k)
b

P_rombu = a*h₁ = b*h₁*k

	ah2		bh1		bh1*(k2+1)
Ptych dwóch trójkątów =		+		=
	2		2		2

I sprawdzamy czy zachodzi: P_{tych dwóch trójkątów} ≥ P_rombu

k2+1
	≥ k
2

k² + 1 ≥ 2k .... dokończ samodzielnie i wyciągnij wniosek

q2: dzieki