Trójkąt, punkty Szkolniak: Dane są punkty A i B. Wyznaczyć zbiór punktów X takich, aby trójkąt AXB był trójkątem ostrokątnym. W zbiorze zadań mam wiele zadań tego typu i sprawiają mi one problem, bo nie wiem jak się za nie zabierać. W jaki sposób w ogóle wyrażać ten 'zbiór'? Rysunkiem? Zapisem? Za co się najpierw zabrać?

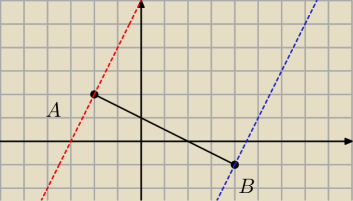
wredulus_pospolitus: propozycja krok 1 −−− odcinek AB krok 2 −−− prostopadła do AB zaczepiona w punkcie A czerwona krok 3 −−− prostopadła do AB zaczepiona w punkcie B niebieska te dwie przerywane ograniczają obszar w którym może być punkt X, tak aby ∡BAX o ∡ABX były mniejsze od 90^o pozostaje tylko wyeliminować obszar w którym ∡AXB ≥ 90^o ... a jak to zrobić ... podpowiem: co wiemy o okręgu opisanym na trójkącie prostokątnym i jak to wykorzystać aby wiedzieć gdzie NIE MOŻE być punkt X (czyli kiedy nie zajdzie, że wspominany kąt jest < 90^o)

Szkolniak: Czyli możemy przyjąć, że naszą przeciwprostokątną jest AB, wyznaczamy środek odcinka AB (niech będzie to punkt S) i zakreślamy okrąg o promieniu r=|AS|=|SB|?

wredulus_pospolitus: dokładnie ... i punkt X nie może leżeć na okręgu (wtedy kąt prosty), ani wewnątrz niego (wtedy kąt rozwarty)

wredulus_pospolitus: Jak już masz graficznie to zapisanie tego za pomocą przedziałów (zbiorów) nie powinno być problemem, prawda

Szkolniak: W takim przypadku czy nie powinniśmy narysować okręgu linią przerywaną? I tak samo z prostymi prostopadłymi do prostej AB? co do pytania − jasne, bez problemu

wredulus_pospolitus: oczywiście −−− okrąg tak samo jak w przypadku prostopadłych −−− linia/krzywa przerywana

Szkolniak: super, dzięki za rozjaśnienie tematu pokombinuje jeszcze z innymi zadaniami tego typu