Wykaż, że: n^m: Wykaż, że:

1
	< log 5 < 1
2

ICSP: Ponieważ √x oraz log(x) są funkcjami rosnącymi to:

1
	= log √10 < log √25 = log 5 < log 10 = 1
2

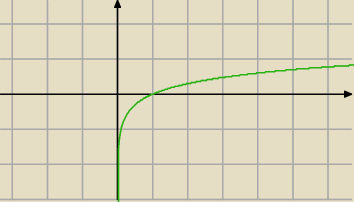a7: 1/2=log√10 1=log10 funkcja logx =log₁0x jest funkcją rosnącą (a>1 podstawa logarytmu większa od 1) czyli wraz ze wzrostem argumentów (iksów) rosną wartości funkcji (ygreki) więc skoro √10 jest mniejszy 5 i 5 jest mniejsze 10 to podana nierówność jest prawdziwa. c.n.u.