Dziwne zadanie
jaros:
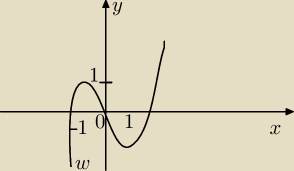
Na rysunku przedstawiony jest wykres funkcji W(x) − ax
3 + bx + c.
Wskaż zależność prawdziwą.
A) a > 0,b > 0, c > 0
B) a > 0, b > 0, c < 0
C) a > 0, b < 0, c < 0
D) a < 0,b < 0, c < 0
Wiem, że c < 0, a > 0 lecz jak mam wyznaczyć b?
24 kwi 19:09
f123: Brak poprawnej odpowiedzi.
24 kwi 19:12
gość: c jest równe 0, bo gdy podstawisz x=0, to dostajesz W(0)=c oraz widać, że dla x=0 funkcja
przyjmuje wartość 0 (z wykresu)

24 kwi 19:13
gość: albo zły wykres albo złe odpowiedzi moim zdaniem
24 kwi 19:14
Eta:
w(0)=c ⇒ c=0
24 kwi 19:14
jaros: C nie jest równe zero, źle narysowałem, jest pod osia x
24 kwi 20:49
ABC:
b wyznaczasz z warunku że funkcja ma dwa ekstrema
24 kwi 21:03
a7: W(1)=a+b+c=0 W(−1)=−a−b+c=0 dodajemy pierwsze i drugie i znowu wychodzi 2c=0 czyli c=0
24 kwi 21:09
a7: a przepraszam, źle odczytałam wykres
24 kwi 21:26
a7:
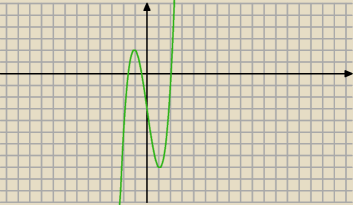
b<0
24 kwi 21:31
jaros: Nie rozumiem zbytnio rozumowania z tym b
24 kwi 21:46
a7: ja zrobiłam ileś wykresów metodą prób i błędów i nie każde b ujemne da ten wykres, ale tylko b
ujemne da ten wykres (skoro, jak piszez a<0, c<0)
24 kwi 21:49
jaros: " ja zrobiłam ileś wykresów metodą prób i błędów i nie każde b ujemne da ten wykres, ale tylko
b
ujemne da ten wykres (skoro, jak piszez a<0, c<0)"
to wreszcie daje ten sam czy nie daje?
24 kwi 21:50
a7:
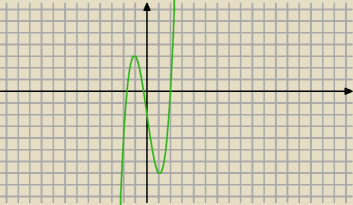
przepraszam a>0
na wykresie y=2x
3−7x−2
24 kwi 21:52
a7: c<0 gdyż dla x=0 W(x)=c, a piszesz, że tam wykres jest poniżej zera czyli c<0
24 kwi 21:54
a7:
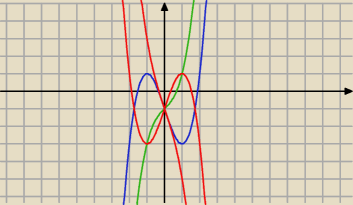
a>0 gdyż inaczej wykres by się zaczynał "od górnego lewego rogu" (czerwone wykresy)
b<0, gdyż inaczej nie byłoby dwóch miejsc zerowych (b>0 zielony wykres)
granatowy wykres a>0 b<0 c<0
24 kwi 21:57
jaros: nie da sie do tego dość algebraicznie?
24 kwi 21:59
a7: nie wiem
c<0 to masz algebraiczne
a>0 to algebraicznie w miarę też logiczne gdyż tylko dla a>0 ujemne iksy dadzą ujemne ygreki

a dodatnie iksy dodatnie ygreki dla a<0 byłoby inaczej
24 kwi 22:12
ite: da się algebraicznie, jeśli chodzi o b, to skorzystaj z podpowiedzi ABC
24 kwi 22:13
a7: f'(x)=3ax
2+b 3ax
2+b=0 x=±
√−b/3a zał na pierwiastek −b/3a>0 to b<0

24 kwi 22:19
jaros: @ite nie do końca rozumiem o co chodzi z tymi 2 ekstremami, mam tam liczyć pochodna z literkami
a i b?
25 kwi 10:58
a7: liczysz pochodną funkcji i wiesz, że ma ona dwa miejsca zerowe, ponieważ miejsce zerowe
pochodnej jest równe
x=√−b/3a lub x=−√−b/3a to pod pierwiastkiem musi być liczba dodatnia (zero nie może być,
gdyż są dwa ekstrema)
−b/(3a) jest dodatnie tylko wtedy gdy b jest ujemne gdyż a jest większe od zera, więc aby cały
ułamek był większy od zera b musi być mniejsze od zera (−b>0 to b<0)
25 kwi 11:16
jaros: Aaaaa, dobrze dziękuje, już rozumiem, to o to chodziło w tym zadaniu

zadanie za 1 pkt a
trudniejsze dla mnie do zrozumienia niż optymalizacyjne XD
25 kwi 11:22
a7: 
25 kwi 11:50
 Na rysunku przedstawiony jest wykres funkcji W(x) − ax3 + bx + c.
Wskaż zależność prawdziwą.
A) a > 0,b > 0, c > 0
B) a > 0, b > 0, c < 0
C) a > 0, b < 0, c < 0
D) a < 0,b < 0, c < 0
Wiem, że c < 0, a > 0 lecz jak mam wyznaczyć b?
Na rysunku przedstawiony jest wykres funkcji W(x) − ax3 + bx + c.
Wskaż zależność prawdziwą.
A) a > 0,b > 0, c > 0
B) a > 0, b > 0, c < 0
C) a > 0, b < 0, c < 0
D) a < 0,b < 0, c < 0
Wiem, że c < 0, a > 0 lecz jak mam wyznaczyć b?

 b<0
b<0
 przepraszam a>0
na wykresie y=2x3−7x−2
przepraszam a>0
na wykresie y=2x3−7x−2
 a>0 gdyż inaczej wykres by się zaczynał "od górnego lewego rogu" (czerwone wykresy)
b<0, gdyż inaczej nie byłoby dwóch miejsc zerowych (b>0 zielony wykres)
granatowy wykres a>0 b<0 c<0
a>0 gdyż inaczej wykres by się zaczynał "od górnego lewego rogu" (czerwone wykresy)
b<0, gdyż inaczej nie byłoby dwóch miejsc zerowych (b>0 zielony wykres)
granatowy wykres a>0 b<0 c<0
 a dodatnie iksy dodatnie ygreki dla a<0 byłoby inaczej
a dodatnie iksy dodatnie ygreki dla a<0 byłoby inaczej

 zadanie za 1 pkt a
trudniejsze dla mnie do zrozumienia niż optymalizacyjne XD
zadanie za 1 pkt a
trudniejsze dla mnie do zrozumienia niż optymalizacyjne XD
