Ocena poprawności komentarza do zadania
Shizzer:
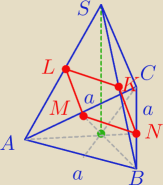
Ostrosłup prawidłowy trójkątny o podstawie ABC i wierzchołku S przecięto płaszczyzną
przechodzącą przez środki krawędzi AC, BC, AS i BS. Pole otrzymanego w ten sposób przekroju
jest cztery razy mniejsze od pola powierzchni bocznej tego ostrosłupa. Oblicz kosinus kąta
nachylenia ściany bocznej do płaszczyzny podstawy.
Nie pytam o rozwiązanie, natomiast chciałbym zapytać się o to czy moje komentarze są
wystarczające i czy uznaliby je za odpowiednie na maturze.
|AC| = |AB| = |CB| = a
|MN| − odcinek łączący środki ramion ΔABC zatem ΔABC ~ ΔCMN z cechy BBB w skali k = 2.
|GH| − odcinek łączący środki ramion ΔABS zatem ΔABS ~ ΔSLK z cechy BBB w skali k = 2.
Więc |GH| = |MN|
Ponadto wszystkie proste zawarte w płaszczyźnie tnącej są do siebie równoległe zatem przekrój
KLMN jest równoległobokiem. Ściany boczne ostrosłupa prawidłowego są przystającymi trójkątami
równoramiennymi dlatego |LM|=|KN| zatem przekrój KLMN jest prostokątem.
Po zapisaniu takiego komentarza byłby on uznany. Byłbym wdzięczny za sprawdzenie.

24 kwi 17:07
Shizzer: To zdanie "Po zapisaniu takiego komentarza byłby on uznany." miało być zapisane tak:
Po zapisaniu takiego komentarza byłby on uznany?
24 kwi 17:07
Shizzer: Sam sobie odpowiedziałem − ten komentarz nie byłby uznany, bo udowodniłem tu, że przekrój
jest równoległobokiem, musiałbym jeszcze jakoś wykazać, że sąsiednie kąty są równe wówczas
byłby to prostokąt.
24 kwi 17:20
Eta:
Dobrze

A odpowiedź do zadania jest
cosα=
√15/6
=========
24 kwi 18:37
Shizzer: Tak, już je rozwiązałem. Dziękuję za sprawdzenie

24 kwi 18:43
Eta:
Tak trzymaj ....

24 kwi 18:49
 Ostrosłup prawidłowy trójkątny o podstawie ABC i wierzchołku S przecięto płaszczyzną
przechodzącą przez środki krawędzi AC, BC, AS i BS. Pole otrzymanego w ten sposób przekroju
jest cztery razy mniejsze od pola powierzchni bocznej tego ostrosłupa. Oblicz kosinus kąta
nachylenia ściany bocznej do płaszczyzny podstawy.
Nie pytam o rozwiązanie, natomiast chciałbym zapytać się o to czy moje komentarze są
wystarczające i czy uznaliby je za odpowiednie na maturze.
|AC| = |AB| = |CB| = a
|MN| − odcinek łączący środki ramion ΔABC zatem ΔABC ~ ΔCMN z cechy BBB w skali k = 2.
Ostrosłup prawidłowy trójkątny o podstawie ABC i wierzchołku S przecięto płaszczyzną
przechodzącą przez środki krawędzi AC, BC, AS i BS. Pole otrzymanego w ten sposób przekroju
jest cztery razy mniejsze od pola powierzchni bocznej tego ostrosłupa. Oblicz kosinus kąta
nachylenia ściany bocznej do płaszczyzny podstawy.
Nie pytam o rozwiązanie, natomiast chciałbym zapytać się o to czy moje komentarze są
wystarczające i czy uznaliby je za odpowiednie na maturze.
|AC| = |AB| = |CB| = a
|MN| − odcinek łączący środki ramion ΔABC zatem ΔABC ~ ΔCMN z cechy BBB w skali k = 2.

 A odpowiedź do zadania jest
cosα=√15/6
=========
A odpowiedź do zadania jest
cosα=√15/6
=========

