Musi być zrobione algebraicznie Amelia: Dwa boki równoległoboku są zawarte w prostych y=1/2x−1 i y=−2/3+6, a jeden z jego wierzchołków ma współrzędne (−1,2). Wyznacz współrzędne pozostałych wierzchołków tego równoległogoku.

Saizou : Przepisz poprawnie treść i podaj swój pomysł na zadanie.

Amelia: Treść jest poprawnie napisana. Doszłam do momentu uzyskania łącznie 3 wierzchołków, czyli brakuje mi jednego. −2/3 x+6=1/2 x−1 i po rozwiązaniu wyszło x=6, a y=2, następnie y=1/2 x+ b 2=1/2* −1 +b i po rozwiązaniu b=2,5, czyli y=1/2 x+ 2,5 i y= −2/3 x + b, następnie 2= −2/3* 6 +b i wychodzi x+3 i y=4 i dalej nie wiem

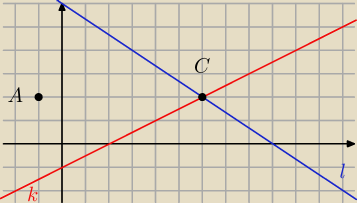
Saizou : 1) Wyznaczyłaś C=(6, 2) 2) prosta m równoległa do l przechodząca przez A 3) Wyznaczenie punktu B jako przecięcia się prostych k oraz m 4) Prosta n równoległa do k przechodząca przez A 5) Wyznaczenie punktu D jako przecięcia się prostych n oraz l

Amelia: Czyli jakie równanie algebraiczne mam ułożyć, aby dowiedzieć się współrzędnych punktu D?

WhiskeyTaster: Zauważ, że skoro dwa boki równoległoboku leżą na prostych

	1
y1 =		x − 1 oraz
	2

	2
y2 = −		+ 6,
	3

to proste, na których będą leżały dwa pozostałe boki muszą być równoległe do y₁ oraz y₂. Innymi słowy znajdź proste, które są równoległe do tych prostych oraz przechodzących przez punkt A = (−1, 2), który z pewnością jest wierzchołkiem równoległoboku, o czym już wiesz. I na koniec szukasz punktów wspólnych odpowiednich prostych W dodatku staraj się zapisywać rzeczy mniej chaotycznie

Amelia: Okey, dziękuję

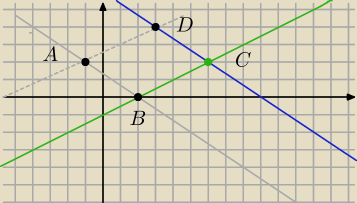
a7: wyznaczamy prostą AB i punkt B prosta AB ma ten sam wsp.kierunkowy a i inne b co prosta DC y=−2/3x+b 2=−2/3(−1)+b b=4/3 y=−2/3x+4/3 dla y=0 x=2 czyli B=(2,0) wyznaczamy prostą AD równoległą do BC y=1/2*x+b A=(−1,2) 2=1/2*1+b b=5/2 y=1/2*x+5/2

	⎧	y=1/2*x+5/2
wyznaczamy punkt D z układu równań	⎩	y=−2/3*x+6	czyli D=(3,4)

	⎧	y=−2/3*x+6
punkt C wyznaczamy z uładu równań	⎩	y=1/2*x−1	C=(6,2)

Amelia: A skąd a7 wiedziałaś, że y=−2/3x+4/3 dla y=0 x=2

a7: racja, prosta AB ma wzór y=−2/3x+b (ten sam wspołczynnik co prosta DC tylko inne B) punkt A należy do tej prostej y=−2/3*x+b współrzędne punktu A są (−1,2) mamy wzór prostej y=−2/3*x+4/3 i sprawdzamy kiedy przetnie się z prostą BC czyli B=(2,0) tak czy siak, ale dzięki za uwagę (chyba zasugerowałam się rysunkiem)

Amelia: a, już wiem, że trzeba znaleźć punkt przecięcia z osią

Amelia: dzięuję za pomoc

a7: nie, nie trzeba znaleźć punkt przecięcia prostych AB i BC wtedy będziemy mieli(miały) punkt B