trapez Kasia: W trapez równoramienny o polu 20 wpisano okrąg o promieniu 2 Oblicz pole czworokąta którego wierzchołkami są punkty styczności okręgu z bokami trapezu

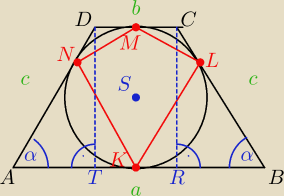
ford: h = 4 (dwa promienie)

a+b
	*4 = 20
2

stąd a+b = 10 z warunku wpisywalności okręgu w czworokąt a+b = c+c stąd ramię trapezu c = 5

	1
|AK| = |AN| = |KB| = |LB| =		a
	2

	1
|DM| = |MC| = |DN| = |CL| =		b
	2

W trójkącie ADT |AT|² + 4² = 5² stąd |AT| = 3 zatem |BR| = 3

	|DT|		4
sinα =		=
	|AD|		5

Kąt NDM = 180^o − α

	4
sin(180o−α) = sinα =
	5

a+b = 10, więc |AT| + |TR| + |BR| + |DC| = 10 3 + |TR| + 3 + |DC| = 10 |TR| + |DC| = 4 |TR| = |DC| = 2 |DN| = |DM| = |MC| = |CL| = 1 |AK| = |KB| = |AN| = |LB| = 4 P_AKN = P_KBL

	1		1		4
PAKN =		*|AK|*|AN|*sinα =		*4*4*		= 6,4
	2		2		5

P_NMD = P_MLC

	1		1		4
PNMD =		*|DN|*|DM|*sin(180o−α) =		*1*1*		= 0,4
	2		2		5

P_KLMN = P_ABCD − P_AKN − P_KBL − P_NMD − P_MCL P_KLMN = 20 − 6,4 − 6,4 − 0,4 − 0,4 P_KLMN = 6,4

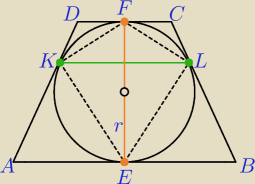Bogdan: Można skorzystać z mało znanej zależności dla trapezu równoramiennego o podstawach a, b i okręgu o promieniu r wpisanego w ten trapez (proponuję samodzielnie ustalić tę zależność). Odcinek łączący punkty styczności okręgu z ramionami trapezu KL ma długość:

	8r2
|KL| =		, gdzie a = |AB|, b = |CD|.
	a + b

	8*22
W tym zadaniu a + b = 10, r = 2, |KL| =		= 3,2 i |EF| = 2r = 4
	10

	1
Pole deltoidu ELFK: PELFK =		*3,2*4 = 6,4
	2

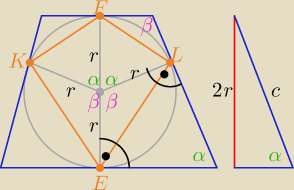Eta: Inny sposób P=20 , h=2r=4 to a+b=10 i a+b=2c ⇒ c=5

	2r		4
sinα=		=		, α+β=180o , to sinβ= sinα
	c		5

	1
P(ELFK)= 4*		*r*r*sinα
	2

P(ELFK)= 6,4 ============

Bogdan:

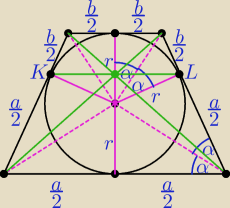
	a		b		ab
Z r2 =		*		=		otrzymujemy
	2		2		4

	8r2		2ab
ab = 4r2 i |KL| =		=		,
	a + b		a + b

KL jest także odcinkiem równoległym do podstaw trapezu i przechodzącym przez punkt przecięcia przekątnych trapezu.

	2*16
W tym zadaniu: ab = 4r2 = 16, |KL| =		= 3,2
	10

Eta:

Bogdan:

Eta:

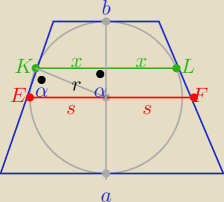
	a+b
s=
	4

x		r		r2		4r2
	=		⇒ x=		⇒ x=
r		s		s		a+b

	8r2
|KL|=2x=
	a+b

===============

Bogdan: