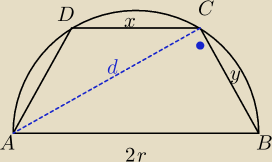
W półkole o promieniu r wpisano trapez równoramienny o przekatnej długosci d. Oblicz długosc
krótszej podstawy trapezu
Trapez rownoramienny jest wpisany w okrag + jeszcze wlasnosci w katach trapezu,wiec
∠ABC = α
∠ADC = 180 − α
∠BAC = 90 − α
∠CAD − 2α − 90
∠ACD = 90 − α
∠ACB = 90 stopni,bo ∠ACB jest oparty na srednicy okregu
| d | |
=2r | |
| sinα |
| d | ||
sinα= | ||
| 2r |
| y | √4r2−d2 | |||
cosα = | = | |||
| 2r | 2r |
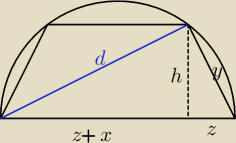z tw. Pitagorasa:
(z+x)2 + h2 = d2 −> d2 − (z+x)2 = h2
z2 + h2 = y2 −> y2 − z2 = h2
czyli:
d2 − (z+x)2 = y2 − z2
oraz wiemy, że: y2 = (x+2z)2 − d2
więc mamy:
d2 − (z+x)2 = (x+2z)2 − d2 − z2
gdzie x + 2z = 2r −−−> z = r − x/2
podstawiasz do wcześniejszego i masz równanie w którym masz 'x' (szukana) oraz 'd' i 'r' (dane)
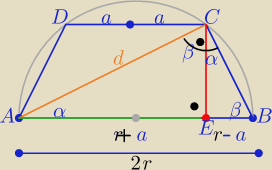Z podobieństwa trójkątów AEC i ABC z cechy (kkk)
| d | 2r | ||
= | ⇒ d2= 2r2+2ar | ||
| r+a | d |
| d2−2r2 | ||
to 2a=|DC|= | ||
| r |
