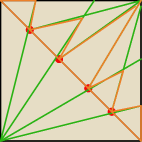
 Bok narysowanego kwadratu wynosi 30. Przekątną kwadratu podzielono na pięć równych części.
Oblicz sumę pol pomaranczowych trójkatów.
Bok narysowanego kwadratu wynosi 30. Przekątną kwadratu podzielono na pięć równych części.
Oblicz sumę pol pomaranczowych trójkatów.
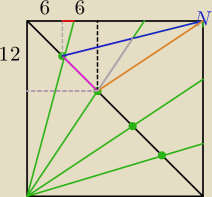 30√2:5=6√2
środkowy najwyższy trójkąt ma pole P=1/2*6√2*15√2=90
dwa małe skrajne mają pole 2*1/2*6*6+1,5)=2*22,5=45
30√2:5=6√2
środkowy najwyższy trójkąt ma pole P=1/2*6√2*15√2=90
dwa małe skrajne mają pole 2*1/2*6*6+1,5)=2*22,5=45
| 9 | ||
dwa średnie mają pole 2*(90−1/2*2*√117* | )≈160 | |
| √109 |
| 30√17 | ||
2*[1/2*30*12−1/2*30*6−1/2*2√117* | ]=180−60√11717 | |
| 17 |
| √17 | ||
wysokość trójkąta o podstawie 2√117 wynosi 30 | , gdyż pole trójkąta o | |
| 17 |