op
f123: Na kole o promieniu 12 opisano trójkąt prostokątny. Oblicz długości boków tego trójkąta,
którego pole jest najmniejsze.
Sprawdzi ktos czy dobrze uzaleznilem 'b' od 'a'
22 kwi 23:04
wredulus_pospolitus:
czym jest a

22 kwi 23:09
f123: bokiem.
22 kwi 23:10
f123:
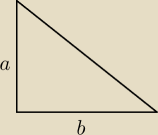
22 kwi 23:10
wredulus_pospolitus:
Prawie:
| | 2P | | ab | | ab | |
12 = r = |
| = |
| = |
| |
| | a+b+c | | a+b+c | | a+b+√a2+b2 | |
22 kwi 23:21
wredulus_pospolitus:
ab − 12(a+b) = 12
√a2+b2
a
2b
2 − 24ab(a+b) + 144(a+b)
2 = 144(a
2 + b
2)
a
2b
2 − 24ab(a+b) = − 288ab
ab − 24b = 24a − 288
22 kwi 23:27
f123: Inaczej to robilem, powinno byc 2ab
22 kwi 23:44
wredulus_pospolitus:
fil
| | ab | |
2P = 2* |
| = ab  |
| | 2 | |
23 kwi 00:00
f123: Robilem z pitagorasa, nie z pola
23 kwi 00:05
wredulus_pospolitus:
pitagoras <−−− jedno równanie
a drugie równanie

23 kwi 00:06
Eta:
@
f123 dobrze

Prostszy zapis:
I dalej już prosto
P(a)
'= 0 ..............
Δ −−− prostokątny równoramienny
a=r(2+
√2) i c= a
√2 = 2r(1+
√2)
============================
23 kwi 01:30
wredulus_pospolitus:
Etuś ... nie jest dobrze.
w sensie −−− jeżeli a,b to BOKI tego trójkąta to nie jest dobrze wyznaczone.
Dobrze jest, jeżeli a+12 i b+12 to są boki tegoż trójkąta

23 kwi 01:36
Eta:
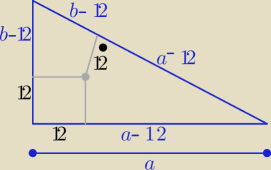
Ja tak bym oznaczała
23 kwi 01:45
Eta:
P=(a−12)(b−12)
i teraz wyznaczyć b z tw .Pitagorasa
gdzie : c= a+b−24
23 kwi 01:47
Eta:
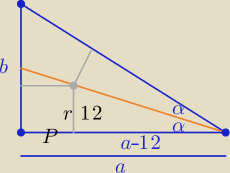
Podam taki sposób:
| | 2tgα | | r | | r(1+tgα) | |
to 2P=a2tg(2α) tg(2α)= |
| i tgα= |
| ⇒ a= |
| |
| | 1−tg2α | | a−r | | tgα | |
podstawiam tgα= t , t>0
| | r2(t+1)2 | | t | |
to: P(t)= |
| * |
| |
| | t2 | | 1−t2 | |
| | r2([t−t2)−(t+1)(1−2t)] | |
P(t) = |
| |
| | t2(1−t)2 | |
P
'(t)=0 ⇒ ...... t
2+2t−1=0
Uzasadnij, że osiąga minimum
dla t=
√2−1
| | 2(√2−1) | |
tgα= √2−1 ⇒ α= 22,5o lub tak tg2α= |
| = ...= 1 |
| | 1−(√2−1)2 | |
to 2α= 45
o
===========
Δ −−− jest prostokątny równoramienny
i dalej już prosto ......
23 kwi 02:27
Eta:
Na rysunku niepotrzebnie "wyskoczyło" P

23 kwi 02:28
wredulus_pospolitus:
Etuś.
Ale co Ty za pole liczysz

P = (a−12)(b−12) to jest pole prostokąta o bokach (a−12) , (b−12),
a przecież:
P
ABC = 12
2 + 12*((a−12) + (b−12))
podstawiając:
a
+ = a − 12
| | 12(a+ + 12) | |
b+ = b − 12 czyli oznaczenia dla których b+ = |
| |
| | a+ − 12 | |
a to pole będzie najmniejsze gdy suma a
+ + b
+ będzie najmniejsza
23 kwi 02:31
Eta:
Punkt styczności dzieli przeciwprostokątną na dwa odcinki x i y
to P
Δ= x*y
Znane Ci to jest ?

23 kwi 02:33
Eta:
Nowe zadanie może brzmieć : wykaż,że tak jest

23 kwi 02:35
wredulus_pospolitus:
Możliwe, że kiedyś było znane

Chociaż nadal bym stwierdził, że zbyteczne jest liczenie pochodnej iloczynu, jeżeli możemy
liczyć pochodną sumy ... odrobinę 'ładniejsza' pochodna wyjdzie
23 kwi 02:36
Eta:
Dla mnie najłatwiej z kątem α

23 kwi 02:37
wredulus_pospolitus:
Faktycznie jest −−− w sumie dowód zajął dwie linijki + wcześniejszy rysunek.
23 kwi 02:43
Eta:

23 kwi 02:48
Eta:
Dobranoc

23 kwi 02:50
Saizou :
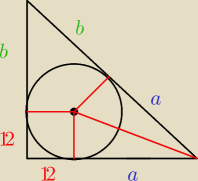
No to bez kątów
| | 1 | |
P(a,b)= |
| (b+12)(a+12)=ab+12b+12a+144 |
| | 2 | |
Pitagoras
(b+12)
2+(a+12)
2=(a+b)
2
24b+144+24a+144=2ab /:2
12a+12b+144=ab
zatem P= P(a,b) = 2ab
NIerówność między średnimi
Równość zachodzi, gdy a=b, zatem trójkąt jest trójkątem prostokątnym równoramiennym.
I dalej już prosto

23 kwi 10:00
f123: To jaki w koncu sposob jest dobry?
23 kwi 10:20
Saizou :
Rozwiążmy, to tak standardowo
Rysunek taki jak u mnie z 10:00
Z tw. Pitagorasa
(b+12)
2+(a+12)
2=(a+b)
2
b
2+12b+144+a
2+12a+144=a
2+2ab+b
2
12a+244=2ab−12b
2(a+144)=2b(a−6)
| | 1 | | a+144 | |
P(a)= |
| ( |
| +12)(a+12) |
| | 2 | | a−6 | |
pochodna itd.
23 kwi 10:32
f123: ale jak ci 'b' takie wyszlo?
23 kwi 10:50
Bleee:
Saizou... Trochę namieszałeś przy wyznaczaniu 'b'.
23 kwi 10:53
f123: Tu chyba najlepiej zrobic pochodna iloczynow, a nie wymnazac cale wyrazenie
23 kwi 10:57




 Prostszy zapis:
Prostszy zapis:

 Ja tak bym oznaczała
Ja tak bym oznaczała
 Podam taki sposób:
Podam taki sposób:

 P = (a−12)(b−12) to jest pole prostokąta o bokach (a−12) , (b−12),
a przecież:
PABC = 122 + 12*((a−12) + (b−12))
podstawiając:
a+ = a − 12
P = (a−12)(b−12) to jest pole prostokąta o bokach (a−12) , (b−12),
a przecież:
PABC = 122 + 12*((a−12) + (b−12))
podstawiając:
a+ = a − 12


 Chociaż nadal bym stwierdził, że zbyteczne jest liczenie pochodnej iloczynu, jeżeli możemy
liczyć pochodną sumy ... odrobinę 'ładniejsza' pochodna wyjdzie
Chociaż nadal bym stwierdził, że zbyteczne jest liczenie pochodnej iloczynu, jeżeli możemy
liczyć pochodną sumy ... odrobinę 'ładniejsza' pochodna wyjdzie



 No to bez kątów
No to bez kątów
