trójkąt Kinga: W trójkącie ABC o bokach AB=12, Bc=10, AC=8 zakreślono okrąg o średnicy AB Okrąg przecina boki BC i AC odpowiednio w punktach D i E W jakim stosunku punkt D dzieli bok BC tego trójkąta

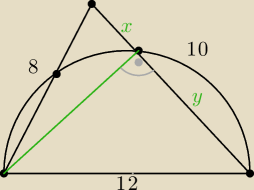
a7: PΔABC=15√7 (wzór Herona) P=1/2*10*h_BC czyli h_BC=3√7 z tw. Pitagorasa x=√10 y=3√10 (√144−54=√90=3√10)

x		1
	=
y		3

a7: w linku wzór Herona na pole trójkąta https://matematykaszkolna.pl/strona/503.html

a7:

	x		1
poprawka x=64−63=1 y=9		=
	y		9

Eta:

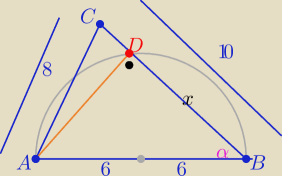
	102+122−82		3
cosα=		⇒ cosα=
	2*10*12		4

	x		3
to w ΔABD cosα=		=		⇒ x=|BD|=9 to |CD|=1
	12		4

|CD| : |DB|=1:9 =============

Eta: Zapomniałam dopisać,że Z tw. kosinusów cosα=......