Trygonometria Kamcio: Chciałem spytać odnośnie rozwiązania zadania, bo nie wiem czy dobrze je zrobiłem, treść brzmi: W trójkącie prostokątnym ABC kąt przy wierzchołku C jest prosty. Wysokość CD dzieli przeciwprostokątna AB na odcinki o długościach 1 i 4. Oblicz tangens większego z kątów ostrych tego trójkata. Nie umiem zrobić na tej stronce za bardzo rysunku więc opiszę: |AD|=1 |BD|=4 △ACD ∼ △ABC

1		|CA|
	=
|CA|		5

|CA|²=5 |CA|=√5 Druga przyprostokątna z Pitagorasa, czyli |BC|= 2√5

	5
tg=
	√5

Leszek: Jest takie twierdzenie ze taka wysokosc : h² = 1*4 ⇒ h =2

Kamcio: A no tak.. faktycznie, dzięki

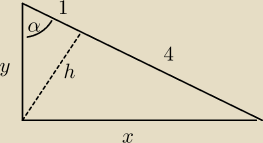
wredulus_pospolitus: 1 + h² = y² 16 + h² = x² oraz: y² + x² = 25 podstawiamy: 1 + h² + 16 + h² = 25 17 + 2h² = 25 2h² = 8 h = 2

	h		2
tgα =		=		= 2
	1		1

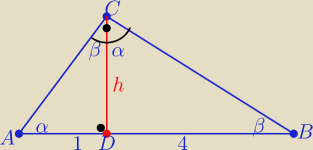
Eta: Z podobieństwa trójkątów ADC i DBC z cechy (kk)

h		4
	=		⇒ h2=1*4 ⇒ h=2
1		h

Eta: Wred.... ale się opisałeś

Leszek: Pani Eta udowodnila to twierdzenie ktore podalem , jest wszystko OK. Cecha podobienstwa Δ (k,k,k)