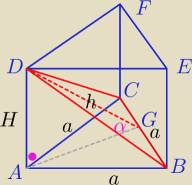
Graniastosłup prawidłowy trójkątny - przekrój i wyznaczenie objętości Shizzer: Graniastosłup prawidłowy trójkątny przecięto płaszczyzną przechodzącą przez krawędź dolnej podstawy i przeciwległy wierzchołek górnej podstawy. Płaszczyzna ta tworzy z podstawą kąt α, a pole przekroju jest równe S. Wyznacz objętość graniastosłupa. Rozwiązuję to zadanie już chyba z piąty raz i wciąż błędnie. Nie potrafię znaleźć błędu w swoich obliczeniach. Czy ktoś mógłby sprawdzić moje rozwiązanie i wskazać błędy? Byłbym bardzo wdzięczny. |AG| to wysokość podstawy zatem:

	a√3
|AG| =
	2

	1
S =		ah
	2

	1
1) Uzależniam h od a, żeby móc skorzystać z warunku S =		ah i uzależnić a od S:
	2

	a√3   2
cosα =
	h

	a√3
hcosα =		/ :cosα
	2

	a√3
h =
	2cosα

2) Uzależniam a od S i kąta α:

	1		1		a√3		√3a2
S =		a * h =		a *		=		/ *4cosα
	2		2		2cosα		4cosα

S4cosα = √3a² / :√3

	S4cosα
a2 =		/ √
	√3

a = √S4cosα / √3 3) Obliczam Pp:

	a2√3		S4cosα		1
Pp =		=		* √3 *		= Scosα
	4		√3		4

4) Obliczam H:

	H
tgα =
	a√3   2

	a√3
H =		tgα
	2

	√S4cosα / √3 * √3		√4Scosα		2√Scosα
H =		* tgα =		* tgα =		* tgα =
	2		2		2

= √Scosα * tgα 5) Obliczam V:

	sinα
V = Pp * H = Scosα * √Scosα * tgα = Scosα *		* √Scosα = Ssinα * √Scosα
	cosα

Poprawna odpowiedź: √S³pierwiastek z 3 * cosα * sinα Nie mam pojęcia skąd mogę taką odpowiedź dostać

Saizou : Sprawdź obliczenie H

Shizzer: Sprawdzałem już to wszystko wcześniej i niestety nie widzę tego błędu

Mila:

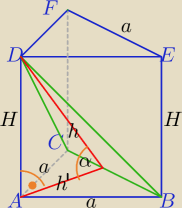
	a2√3
V=		*H
	4

1) P_BCD=S

	a*h
S=
	2

	2S
a*h=2S⇔h=
	a

2)

	a√3
h'=
	2

	h'
cosα=		⇔h'=h*cosα
	h

a√3		2S
	=		*cosα /*(a /2)
2		a

a2√3
	=S * cosα=PABC
4

Stąd a²:

a2√3
	=S * cosα /*4√3
4

3a²=4√3S*cosα

	√4√3 *S*cosα
a=
	√3

3) Teraz wysokość H

	H
sinα=
	h

	2S		√3*sinα		2S√3*sinα√4√3 S*cosα
H=h*sin α=		=2S*		=
	a		√4√3 *S*cosα		4√3S cosα

	sinα*√4√3 Scosα
H=
	2 cosα

	sinα*2√√3 Scosα
V=S*cosα*
	2 cosα

V=S*sinα*√√3 S*cosα V=sinα*√S³ √3*cosα ================

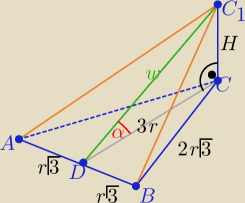Eta: A ja z trójkąta "ekierki" (30^o,60^o,90^o) ( oznaczenia na rys. Obliczenia stają się bardziej przyjazne P_p=3r²√3

	3r
S=r√3*w , w=		i H= 3r*tgα
	cosα

S*cosα=3r²√3 ⇒ 9r²=S√3cosα to r= √S√3cosα/3 V= P_p*H V= 9r²√3*r*tgα

	√S√3cosα
V= S√3cosα*√3*		* tgα
	3

V= √S³√3cosα*sinα ==================

Shizzer: Dziękuję za pomoc. A czy ktoś może widzi gdzie popełniam błąd w obliczeniach?

Mila: Ekierka jest dobra na wszystko A ja jakoś ciągle ją omijam.

Mila: Jutro przeliczę Twoje rachunki, to napiszę

Shizzer: Super! Bardzo mi się przyda, bo szło zwariować dziś z robieniem akurat tego zadania

Eta:

Mila: Wszystko ładnie i Twój sposób bardziej mi się podoba niż mój, tylko zgubiłeś √3 w ostatnim przekształceniu punkt (4). Piszę tylko licznik, bo w tym edytorze nic nie widać: Włączając √3 pod pierwiastek masz tak: √4S cosα*√3=√4S*3cosα −to jest nowy licznik Pod pierwiastkiem masz teraz :

4S*3 cosα
	=4S*√3*cosα
√3

	1
H=√4S√3*cosα*		*tgα
	2

H=√S*√3*cosα *tgα ================= Popatrz na sposób Ety, bo może będzie to dla Ciebie prostsze.

Shizzer: No tak! Dziękuję za wyłapanie błędu. Zrobię to zadanie jeszcze raz swoim sposobem,a jutro przeanalizuję sposób Ety, bo choć bardzo ciekawy to 23:26 nie jest dobrą porą, żeby starać się go zrozumieć w moim przypadku

Mila: Dobranoc

Shizzer: Dobranoc