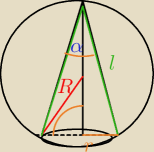
 Pb=πrl
Pk=4πR2
PbPk = 38 = πrl4πR2
8rl=12R2
2rl=3R2
No i nie wiem co dalej.
Pb=πrl
Pk=4πR2
PbPk = 38 = πrl4πR2
8rl=12R2
2rl=3R2
No i nie wiem co dalej.
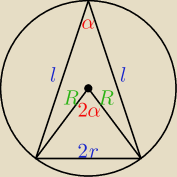 a teraz
a teraz 
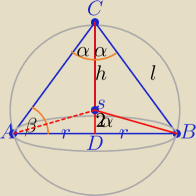
 z tw. cosinusów:
l2 = 2R2(1 + cosα)
(2r)2 = 2R2(1 − cos(2α))
zauważ także, że masz z proporcji pól:
2rl = 3R2 −−−>
4r2 * l2 = 9R4
2R2(1 − cos(2α)) * 2R2(1 + cosα) = 9R4
4(1−cos(2α))(1−cosα) = 9
ciągnij to dalej
z tw. cosinusów:
l2 = 2R2(1 + cosα)
(2r)2 = 2R2(1 − cos(2α))
zauważ także, że masz z proporcji pól:
2rl = 3R2 −−−>
4r2 * l2 = 9R4
2R2(1 − cos(2α)) * 2R2(1 + cosα) = 9R4
4(1−cos(2α))(1−cosα) = 9
ciągnij to dalej
| π | ||
0<α< | ||
| 2 |
| πr l | 3 | r*l | 3 | |||||
1) | = | ⇔ (* ) | = | |||||
| 4πR2 | 8 | R2 | 2 |
| 2r | |
=2R⇔r=R*sin(2α) | |
| sin(2α) |
| l | |
=2R | |
| sinβ |
| R*sin(2α)*2R cos α | 3 | |||
= | ||||
| R2 | 2 |
| 3 | ||
2sin(2α)*cosα= | ||
| 2 |
| 3 | ||
sin(2α)*cosα= | ||
| 4 |
| 3 | ||
2sinα*cos2α= | ||
| 4 |
| 3 | ||
sinα*(1−sin2α)= | ||
| 8 |
| 3 | ||
t*(1−t2)= | ||
| 8 |
| 3 | 1 | |||
t3−t+ | =0 sprawdzamy dla t= | |||
| 8 | 2 |
| 1 | 1 | 3 | ||||
L= | − | + | =0 | |||
| 8 | 2 | 8 |
| 1 | ||
sinα= | ||
| 2 |
| π | ||
α= | ||
| 6 |
| π | ||
2α= | ||
| 3 |
| 3 | 1 | 1 | 3 | |||||
(t3−t+ | ): ((x− | =(t2+ | t− | ) | ||||
| 8 | 2 | 2 | 4 |
| 1 | 3 | |||
(t2+ | t− | )=0 − odrzuć rozw. ujemne, a dodatnie sprawdź , | ||
| 2 | 4 |