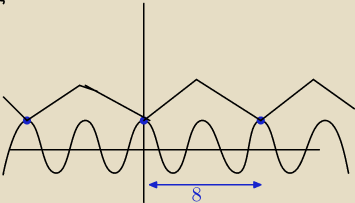
funkcje ao: Hej, czy mogę powiedzieć, że takie funkcje (wiem że dziwnie wyglądają, chodzi o samą zasadę) mające rozwiązania co naprzykład 8x mają nieskończenie wiele rozwiązań?

PW: Funkcje mające rozwiązania...? A poprawnie umiesz powiedzieć o co idzie?

ao: chodzi o to, że dane funkcje jak np wyżej mają rozwiązania okresowe, no np cos(x)=1, wtedy jakby wykresy tych funkcji przecinają się co kπ więc rozwiązaniami tych dwóch funkcji są liczby postaci x=kπ, no i wiadomo, że zarówno f(x)=1 oraz f(x)=cosx biegną od + do − ∞ więc tych rozwiązań będzie bardzo dużo, czy w takim razie mogę stwierdzić, że równanie cosx=1 ma nieskończenie wiele rozwiązań?

PW: Nie ma czegoś takiego jak "rozwiązanie funkcji". To że równanie4 cosx = 1 ma nieskończenie wiele rozwiazań wynika z okresowości funkcji cos(x).

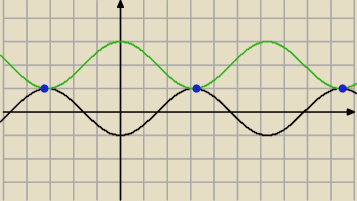
a7: chyba chodzi Ci o rozwiązania równań jak np. powyżej −cosx = cosx+2 to , o ile wiem, owszem, można jak najbardziej tak powiedzieć ( i tak zilustrować), że mają nieskończoną ilość rozwiązań

a7: jeśli natomiast chodzi Ci o sygnał trójkątny i rozwijanie go w szereg Fouriera to nie wiem czy tak można powiedzieć