trojkat trójmistrz: Dlaczego w obu trójkątach te kąty są identyczne? https://zapodaj.net/5616cf3a6aede.png.html

Leszek: Bo trojkaty ABO i ABC sa podobne ( k,k,k)

trójmistrz: W jaki sposób? To rodzi więcej pytań niż odpowiedzi...

Leszek: Przeciez masz rownolegle przesuniecia , dorysuj bok AB i zobaczysz katy odpowiednio takie same w tych dwoch trojkatach .

Leszek: Wektor v{A) rownoleglu do AB , i.td

Jerzy: Bo v_a jest równoległy do wektora BC

Leszek: Sorry , v_A | | BC , AB || BD

trójmistrz: No właśnie, o ile widzę, że v_a || BC, to już AB || BD nie jest takie oczywiste

trójmistrz: Czy może robię błąd i sugeruję się obrazkiem? Bo gdyby Δs była faktycznie mała, to AB faktycznie mogłoby być równoległe do BD

Jerzy: AB nie jest równoległe do BD

Jerzy: Natomiast 19:31 zawsze.

Leszek: Zauwasz ,ze wektor v_A jest prostopadly do r i odcinek BD tez jest prostopadly do r .

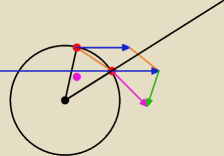
trójmistrz: Ech, człowiek tak czasem kombinuje, że głowa mała, a tu wystarczy pomyśleć. Rysunek nie za super, ale tak: jeśli przesunąć wektor v_A tak, by leżał na jednej prostej, na której leży punkt B, to przecięcie tej prostej z odcinkiem OA będzie tworzyło kąt prosty. No to utworzony tak trójkąt prostokątny ma kąty: α, 90, 90 − α. Kąt 90 − α jest kątem wierzchołkowym z tym tworzonym przez przedłużenie odcinka OB oraz wektor BC. I teraz z prostopadłości wektora stycznego do promienia w punkcie B mamy 90 − α + x = 90, stąd x = α. Chaotycznie, ale zgadza się?

Leszek: Tak ,jest OK.

trójmistrz: Dziękuję za cierpliwość