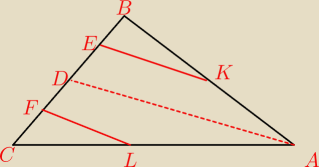
Na bokach AB i AC trójkąta ABC wybrano odpowiednio punkty K i L w ten sposób, że |BK | =
|AL | . Punkt D jest środkiem odcinka BC . Przez punkty K i L poprowadzono proste
równoległe do AD , które wyznaczyły na boku BC punkty E i F odpowiednio (zobacz rysunek).
Wykaż, że jeżeli |BC | = 2|EF| , to |AB | = |AC | .
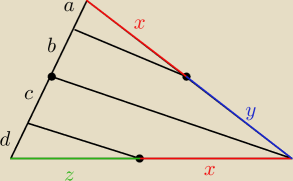Z warunków zadania
b+c=a+d
d+c=b+a
======−
b−d=d−b
d=b oraz c=a (*)
z tw. Talesa
| a | b | bx | |||
= | →y= | ||||
| x | y | a |
| d | c | dx | |||
= | →z= | ||||
| z | x | c |
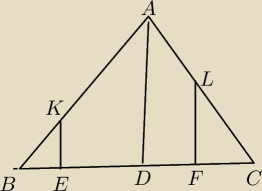LC=a
AL=x
BK=x
KA=b
DF+FC=ED+BE oraz DF+ED = FC + BE
z tego
DF+FC=ED+BE
DF−FC=BE−ED
DF=BE
DF+BE=FC +BE
DF=FC
| 1 | ||
FC= | DC oraz ED=FC | |
| 2 |
| x | b+x | ||
= | ⇒b=x | ||
| y | 2y |
| a | |
={a+x}{2y} ⇒ a=x | |
| y |
