Sprawdzenie zadań z prawd. kombinatoryki, f.kwadratowej
Jokur: 1) Ośmiu chłopców i pięć dziewczynek ustawiamy w szeregu w sposób losowy. Oblicz
prawdopodobieństwo zdarzenia: Żadne dwie dziewczynki nie stoją obok siebie
Wyszło mi Ω=13! A=5!*8!*13
| | | |
A w odp. A= 5!*8!* | i nie rozumiem do końca dlaczego |
| | |
2) Dane jest równanie: x+y+z=8
a) Wyznacz ilość wszystkich rozwiązań postaci (x,y,z) podanego równania wiedząc, żę x,y,z
∊N
+
b) Wyznacz ilość wszystkich rozwiązań postaci (x,y,z) podanego równania wiedząc, żę x,y,z
∊N
w a) wyszło mi 21 możliwości i czy należy tą ilość pomnożyć razy 3 z racji, że liczby między
sobą mogą się różnić?
anlagoiczne zapytanie do b) i czy jest jakaś szybsza metoda na zliczenie tego niż rozpisywanie
kolejnych możliwości?
3) Dla jakich wart. parametru m (m∊R) jeden z pierwiastków równania: x
2+m=12x jest o 2
√5
większy od drugiego?
Wystarczy jak zapiszę sobie warunek x
1=x
2+2
√5 i podstawię do wzoru Viete'a na sumę?
Otrzymuję wtedy gotowe miejsca zerowe i wymnażam ze sobą i porównuję z początkowym równaniem
dostając ostateczny wynik m=31, czy muszę rozpatrywać jeszcze Δ oraz wzór Viete'a na iloczyn?
21 kwi 13:36
janek191:
1)
CC DCDCDCDCD CC
21 kwi 16:43
Jerzy:
@ Janek191,a dlaczego wykluczsz możliwość,że dwóch chłopców stoi między dziewczynkami ?
21 kwi 17:05
janek191:
Nawet 3 lub 4 lub 5 może stać pomiędzy dwoma dziewczynkami.
DCCCDCDCDCDCC
DCCCCDCDCDCDC
DCCCCCDCDCDCD
21 kwi 17:14
Jerzy:
16:43, to najwyraźniej jeden schemat.
21 kwi 19:09
Jokur: | | | |
Poprawna odpowiedź to 5!*8!* | , tylko kombinacja sugeruje, że nieważne na jakich 5 |
| | |
miejscach ustawimy dziewczynki, więc równie dobrze mogą stać obok siebie i nie wydaję mi się
aby ten sposób był dobry
Chyba, że mój tok myślenia jest błędny
22 kwi 15:24
wredulus_pospolitus:
Jokur
krok 1: ustawiamy chłopaków jeden za drugim: 8! sposobów
krok 2: nakazujemy chłopakom się rozsunąć tak, że pomiędzy każdym z nich jest miejsce dla
jednej osoby + jedno miejsce przed pierwszym + jedno miejsce za ostatnim −−− daje nam to
łącznie 9 miejsc.
| | | |
krok 3: z tych 9 miejsc wybieramy 5 które zajmą dziewoje: | |
| | |
krok 4: permutujemy dziewoje: 5!
22 kwi 15:28
wredulus_pospolitus:
I dokładnie taki sposób myślenia proponuję do tego typu zadań (a co pewien czas one wracają na
maturze)
22 kwi 15:28
wredulus_pospolitus:
Co do zadania (2) −−−− NIE ... niewiadome x,y,z NIE SĄ ROZRÓŻNIALNE.
W tym zadaniu mogłeś skorzystać z kombinacji z powtórzeniami.
Co do zadania (3) −−− musisz sprawdzić czy Δ>0, ponieważ wzory Viete'a "działają jeżeli masz
dwa rozwiązania".
22 kwi 15:33
Jokur: Dziękuję bardzo za jasne wytłumaczenie
Jak należałoby rozpisać kombinację w 2) bo ja liczyłem to "na piechotę" rozpisując kolejne
przypadki
22 kwi 16:07
wredulus_pospolitus:
Po namyśle −−− chciałbym zaproponować inne podejście do tematu:
można do tego (2) podejść w takim sposób:
masz 8x '1' ustawione jedna za drugą ... pomiędzy nimi (7 miejsc) masz miejsca do wstawienia
maksymalnie jednej

przegrody (a wstawić masz dwie sztuki).
Twoim zadaniem jest policzenie na ile sposobów możesz umieścić te przegrody.
| | 7*6 | |
Odpowiedź: Na |
| = 21 sposobów. |
| | 2 | |
Uwaga −−− tutaj kolejność jest istotna, ponieważ x=2, y = 1, z=5 oraz x = 2, y = 5, z = 1
traktujesz jako dwa osobne przypadki
Zastanów się jak 'przekształcić' powyższą metodę dla podpunktu (b).
22 kwi 16:35
Jokur: Wybacz, ale kompletnie nie rozumiem tego sposobu, próbowałem to sobie rozpisać na kartce ale
też z marnym skutkiem.
Dlaczego akurat 8x '1' i dlaczego ustawiamy to jedna za drugą?
22 kwi 18:27
wredulus_pospolitus:
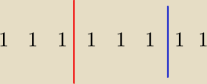
aby uzyskać coś takiego.
przegrody czerwona i niebieska podzieliły te 8x jedynek na trzy grupy
x = 1+1+1 = 3
y = 1+1+1 = 3
z = 1+1 = 2
i stąd otrzymujemy jedną z możliwości czyli układ (3,3,2)
Teraz policz ile w sumie jest taki możliwości −−− zauważ, że o ile na rysunku te przegrody są
innego koloru (czerwona i niebieska) to tak naprawdę są one NIEROZRÓŻNIALNE, stąd to dzielenie
przez 2 o godzinie 16:35
22 kwi 18:37
Jokur: O jasny gwint, pierwszy raz widzę na oczy taki sposób i w sumie podoba mi się− łatwy i mający
dużo zastosowań.
Rozumiem, że można też zrobić coś podobnego dla 4,5,6 itd liczb
22 kwi 18:53
Mila:
Zadanie1)
Jokur sposób podany przez
Janka jest bardzo prosty
Ośmiu chłopców i pięć dziewczynek
1) Ustawiasz ośmiu chłopców
⋁C1⋁C2⋁C3⋁C4⋁C5⋁C6⋁C7⋁C8⋁
Masz (8+1)=9 miejsc na których może stanąć dziewczynka
| | 9! | | 5!*6*7*8*9 | | 6*7*8*9 | |
= |
| = |
| = |
| =126 |
| | 5!*(9−5)! | | 5!*4! | | 1*2*3*4 | |
Teraz należy uwzględnić wszystkie możliwe ustawienia
8! −na tyle sposobów możesz ustawić w rzędzie 8 osób
5! − na tyle sposobów ustawić w rzędzie 5 osób
=========
Czyli masz wynik :
| |
*8!*5!=126*8!*5! i taki wynik zostaw. |
| |
Dla ciekawości :
wynik:
609 638 400 możliwości, więc raczej długo byś liczył na piechotę i raczej z błędem by było.
22 kwi 21:29
Mila:
Zadanie 2,3 już jasne?
22 kwi 21:29
Jokur: Przepraszam, że odpowiadam dopiero po tygodniu, ale trochę miałem na głowie.
Dziękuję bardzo
Mila za dokładniejsze wyjaśnienie i tak wszystko już jasne.
Dziękuję raz jeszcze wszystkim za pomoc!

29 kwi 21:09
Mila:

29 kwi 22:45
zbyszko 3 cytryny: siema siema wariaty eluwina
19 maj 23:36
 przegrody (a wstawić masz dwie sztuki).
Twoim zadaniem jest policzenie na ile sposobów możesz umieścić te przegrody.
przegrody (a wstawić masz dwie sztuki).
Twoim zadaniem jest policzenie na ile sposobów możesz umieścić te przegrody.
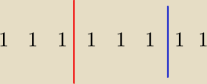 aby uzyskać coś takiego.
przegrody czerwona i niebieska podzieliły te 8x jedynek na trzy grupy
x = 1+1+1 = 3
y = 1+1+1 = 3
z = 1+1 = 2
i stąd otrzymujemy jedną z możliwości czyli układ (3,3,2)
Teraz policz ile w sumie jest taki możliwości −−− zauważ, że o ile na rysunku te przegrody są
innego koloru (czerwona i niebieska) to tak naprawdę są one NIEROZRÓŻNIALNE, stąd to dzielenie
przez 2 o godzinie 16:35
aby uzyskać coś takiego.
przegrody czerwona i niebieska podzieliły te 8x jedynek na trzy grupy
x = 1+1+1 = 3
y = 1+1+1 = 3
z = 1+1 = 2
i stąd otrzymujemy jedną z możliwości czyli układ (3,3,2)
Teraz policz ile w sumie jest taki możliwości −−− zauważ, że o ile na rysunku te przegrody są
innego koloru (czerwona i niebieska) to tak naprawdę są one NIEROZRÓŻNIALNE, stąd to dzielenie
przez 2 o godzinie 16:35

