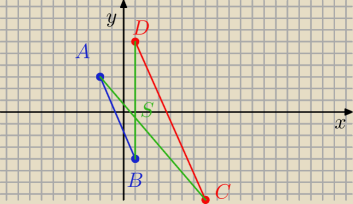
jednokładność m: Obrazem odcinka AB, gdzie A(−2,3), B(1,−4) w jednokładności o środku S i skali k<0 jest odcinek CD, w którym C(7,−8) oraz D(1,6). Wyznacz środek i skalę jednokładności

janek191: I AB I² = 3² + 7² = 9 + 49 = 58 I AB I = √58 I CD I² = 6² + 14² = 36 + 196 = 232 I CD I = √232 I k I = I CD I : I AB I = √232 : √58 = √4 = 2 k = − 2 ====== Dokończ S = ( x , y) pr. AC wyznacz pr BD : x = 1

m: pr. AC: y=⁻¹¹₉ x + ⁵₉ nie wiem jak wyliczyć pr. BD i nie wiem co dalej? Nigdy nie robiłam tego metodą prostych, tylko wektorami (tylko coś zapomniałam jak to się robi).

janek191: B = ( 1, − 4) D = ( 1, 6 ) więc prosta BD ma równanie x = 1 bo taka prosta przechodzi przez te punkty.

janek191:

	2
S = ( 1, −		)
	3

janek191: Można za pomocą wektorów. S = ( x, y) → → CS = 2 SA [ x − 7 , y + 8 ] = 2 *[ −2 − x, 3 − y ] = [ − 4 −2 x , 6 − 2 y] więc x − 7 = − 4 − 2 x 3 x = 3 x = 1 oraz y + 8 = 6 − 2 y 3 y = − 2

	2
y = −
	3

	2
S = ( 1, −		)
	3

============