Oblicz przekątną równoległoboku. Mcj: Oblicz krótszą przekatną równoległoboku, wiedząc, że kąt ostry równoległoboku ma miarę 30 stopni, obwód wynosi 24 a pole 16.

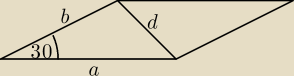
Bogdan: ab*sin30^o = 16 ⇒ ab = 32 i a + b = 12, a > 0 i b > 0. Rozwiąż ten układ równań, otrzymasz długości a oraz b, długość d można wyznaczyć korzystając np. z twierdzenia cosinusów

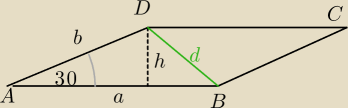
a7: sin30=1/2 h/b=1/2 b=2h a*h=16 2a+2b=24 czyli 2a+4h=24 czyli a=12−2h a*h=16 czyli (12−2h)h=16 12h−2h²=16 h²−6h+8=0 h_a=2 lub h_b=4 a=8 b=4 z tw. cosinusów d²=a²+b²−2abcosα

	√3
d2=82+42−2*8*4*		czyli d=√80−24√3=2√20−6√3
	2

Mcj: Pod koniec jest błąd rachunkowy. 8*4 to 32 wiec wynik 4√5−2√3

Mcj: Dziękuję bardzo za pomoc. 👍👍👍

Bogdan: wyznaczenie h nie było potrzebne

Bogdan: b = 12 − a ab = 32 ⇒ 12a − a² = 32 ⇒ a² − 12a = −32 ⇒ a² − 12a + 36 = −32 + 36 (a − 6)² = 4 ⇒ a − 6 = −2 lub a − 6 = 2 ⇒ a = 4 i b = 8 lub a = 8 i b = 4