Sprawdzenie rozwiązania zadania z ostrosłupem Shizzer: Podstawą ostrosłupa jest trapez równoramienny o kącie ostrym α, w którym ramię i krótsza podstawa ma długość a. Każda krawędź boczna ostrosłupa tworzy z płaszczyzną podstawy kąt β. Oblicz objętość tego ostrosłupa. Prosiłbym, żeby ktoś sprawdził czy dobrze rozwiązałem to zadanie. Jeśli źle to byłbym wdzięczny gdyby osoba sprawdzająca wytknęła błąd, który spowodował błędną odpowiedź. Mam prawidłową odpowiedź do tego zadania, ale odpowiedź jest oczywiście podana jako iloczyn stałych i funkcji trygonometrycznych dlatego poprawnych odpowiedzi może być zapewne wiele, lecz inaczej sformułowanych. Odpowiedź z książki: (√2/6)a³√(1 + cosα)³tgβ Moje rozwiązanie: Krawędzie boczne są nachylone pod tym samym kątem β do płaszczyzny podstawy zatem na podstawie możemy opisać okrąg, którego środkiem jest spodek wysokości ostrosłupa. Dodatkowo wszystkie krawędzie boczne są równej długości. 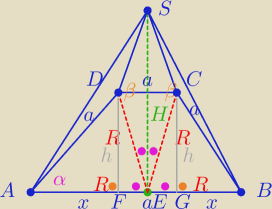Rysunek może nie być czytelny dlatego zapiszę miary kątów i odcinków. |CD| = |AD| = |CB| = |FG| = a |AE| = |DE| = |CE| = R |∡DFA| = |∡CBG| = α |∡SAE| = |∡EDS| = |∡ECS| = |∡EBS| = β Z funkcji trygonometrycznych dla ΔAFD: sinα = ^h_a ⇒ h = asinα |AB| = b b = 2x + a Z funkcji trygonometrycznych znów dla ΔAFD: cosα = ^x_a ⇒ x = acosα ⇒ b = a + 2acosα Pp = ^{a + a + 2acosα}₂ * asinα = ^{2a + 2acosα}₂ * asinα = a(1 + cosα) * asinα = a²sinα(1 + cosα) Tej części nie jestem pewny. Obliczam R z tw. kosinusów dla ΔDAE: R² = a² + R² − 2aRcosα R² − R² + 2aRcosα = a² a² = 2aRcosα / :2acosα (Wydaje mi się, że w tym miejscu może być błąd, bo dla α=45^o dzielę tu przez 0) Skoro raczej nie mogę policzyć tego R z twierdzenia kosinusów to jak inaczej do tego podejść?

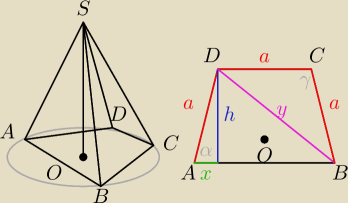Saizou : 1) Założyłeś, że trapez ABCD jest trapezem równoramiennym o kącie ostrym 45^o.

	√2
2) dla α=45o, cosα=		wiec nie jest to zero
	2

	x
cosα=		→ x=acosα
	a

	h
sinα=		→ h=asinα
	a

	1
Pp=		(2a+2acosα)asinα=a2(1+cosα)sinα
	2

ΔBCD jest równoramienny (γ=180−α (suma miar kątów przy jednym ramieniu trapezu)), zatem

	1
∠BDC =∠CBD=		α
	2

Promień okręgu opisanego na trapezie ABCD jest promieniem okręgu opisanego na trójkącie BCD

a
	=2R
1   sin α   2

	a
R=
	1   2sin α   2

i dalej samemu

Shizzer: Nie założyłem, że trapez ABCD musi mieć kąt 45^o jeśli jest równoramienny tylko miałem zaćmienie mózgu i pomyślałem, że cosα=0 dla α=45^o, a to oczywiście głupota Kontynuując rozwiązanie:

	H
tgβ =
	R

H = Rtgβ

	atgβ
H =
	α   2sina   2

	1		atgβ
V =		* a2sinα(1 + cosα) *		=
	3		α   2sin   2

	1		a3sinαtgβ(1 + cosα)
=		*		=
	3		α   2sin   2

	1		α   α   a32sin cos tgβ(1 + cosα)   2   2
=		*		=
	3		α   2sin   2

	1		α
=		* a3cos		tgβ(1 + cosα)
	3		2

Czy wynik jest ok?

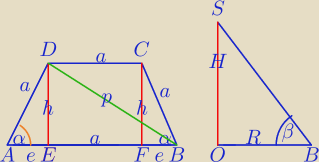Mila: Bez rysunku ostrosłupa 1) W ΔAED:

	e
cosα=		⇔e=acosα
	a

|AB|=2acosα+a=a*(2cosα+1)

	h
sinα=		⇔h=asinα
	a

	2acosα+a+a
PABCD=		*a sinα
	2

P_ABCD=(acosα+a)*asinα= a²*(cosα+1)*sinα 2) Spodek wysokości ostrosłupa leży w środku okręgu opisanego na ABCD

p
	=2R
sinα

W ΔDEB: p²=|EB|²+h² p²=(a+a cosα)²+(asinα)²=a²*(1+cosα)²+a²sin²α p²=a²*(2+2cosα) p=a√2*√1+cosα

	a√2*√1+cosα)
R=
	2sinα

3) W ΔSOB:

	H
tgβ=
	R

H=R*tgβ=U{a√2*√1+cosα){2sinα} 4)

	1		a√2*√1+cosα)
V=		*a2*(cosα+1)*sinα*		*tgβ
	3		2sinα

	a3*√2(cosα+1)√cosα+1*tgβ
V=		⇔
	6sinα

	a3*√2*√(cosα+1)3*tgβ
V=
	6sinα

========================

Shizzer: Dziękuję za pomoc

Saizou : To ja dokończę swoją

	H		a
tgβ=		⇒ H = R*tgβ =		*tgβ
	R		α   2sin   2

	1		a
V =		* a2(1+cosα)sinα *		* tgβ=
	3		α   2sin   2

	1		α		α		α		1
=		a3 * tgβ * 2cos2		* 2sin		cos		*		=
	6		2		2		2		α   sin   2

	1		α
=		a3 * tgβ * 4cos3		= (*)
	6		2

	1		1+cosα
=		a3 * tgβ * 4(√		)3=
	6		2

	√2
=		a3 * √(1+cosα)3 * tgβ
	6

Chociaż (*) ładniej wygląda