| EB | BF | ||
+ | =1. | ||
| AE | FC |

 Szkic:
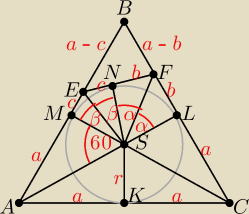
Założenia: |BM| = |MA| = |AK| = |KC| = |CL| = |LB| = a = r√3,
|KS| = |LS| = |NS| = |MS| = r, |LF| = |FN| = b, |NE| = |EM| = c,
|BF| = a − b, |BE| = a − c,
|∡MSA| = |∡KSA| = |∡KSC| = |∡LSC| = 60o, |∡LSF| = |∡NSF| = α, |∡NSE| = |∡MSE| = β
Szkic:
Założenia: |BM| = |MA| = |AK| = |KC| = |CL| = |LB| = a = r√3,
|KS| = |LS| = |NS| = |MS| = r, |LF| = |FN| = b, |NE| = |EM| = c,
|BF| = a − b, |BE| = a − c,
|∡MSA| = |∡KSA| = |∡KSC| = |∡LSC| = 60o, |∡LSF| = |∡NSF| = α, |∡NSE| = |∡MSE| = β
| a − c | a − b | |||
Teza: | + | = 1 | ||
| a + c | a + b |
| tg60o − tgα | √3 − tgα | |||
tgβ = tg(60o − α) = | = | |||
| 1 + tg60o*tgα | 1 + √3*tgα |
| a−c | a−b | r√3 − r*tgβ | r√3 − r*tgα | ||||
+ | = | + | = | ||||
| a+c | a+b | r√3 + r*tgβ | r√3 + r*tga |
| √3 − tgβ | √3 − tgα | |||
= | + | = ... (dalej samodzielnie) .. = 1 | ||
| √3 + tgβ | √3 + tgα |