zadanie panda: Czy to zadnie z rombem da sie wogole rozwiązać, bo mi się wydaje bardzo trudne: Niech ABC bedzie trójkatem, w którym |AB|=44, |BC|=28, |CA|=36. Na bokach AB, BC,AC wybieramy odpowiednio punkty F,E,D, tak że CFED jest rombem. Oblicz bok tego rombu.

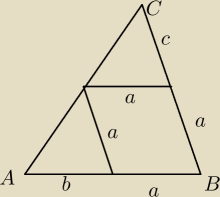
wredulus_pospolitus: a+c = 28 a+b = 36

c		a
	=		⇔ a2 = b*c (z podobieństwa trójkątów)
a		b

trzy równania ... trzy niewiadome ... rozwiązujesz takie równanie kwadratowe: a² = (28−a)(36−a)

Mila: Panda popraw treść, bo te punkty F,E,D inaczej wg mnie trzeba ułożyć .

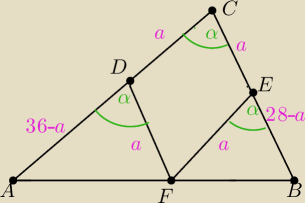
a7: PΔABC=1/2(36−a)*a*sinα+a²sinα+1/2a(28−a)sinα=1/2*36*28sinα \mnożymy razy 2, dzielimy przez sinα (36−a)*a+2a²+a(28−a)=36*28 36a−a²+2a²+28a−a²=1008 64a=1008 a=15,75